
6.5 Оценивание неизвестных параметров распределения
Подпункты этого параграфа:
Предположим, что
![]() -- независимая выборка из неизвестного
распределения
-- независимая выборка из неизвестного
распределения
![]() , зависящего от неизвестного параметра
, зависящего от неизвестного параметра
![]() .
Часто возникает необходимость приблизить значение некоторой функции
.
Часто возникает необходимость приблизить значение некоторой функции
![]() от параметра
от параметра ![]() . Функция
. Функция
![]() , вообще говоря, может
принимать векторные значения:
, вообще говоря, может
принимать векторные значения:
Нередко рассматривают ситуацию ![]() ,
,
![]() . В этом
случае говорят просто об оценке неизвестных параметров распределения, которую
принято обозначать
. В этом
случае говорят просто об оценке неизвестных параметров распределения, которую
принято обозначать
Сразу возникают три вопроса: какие оценки можно считать хорошими; как сравнивать две оценки по качеству; как строить оценки. Начнем с первого из них.
Какие оценки можно считать хорошими ?
Оценка
![]() называется несмещенной
для функции от неизвестного параметра
называется несмещенной
для функции от неизвестного параметра
![]() , если
, если
Рассмотрим статистическую модель Примера 6.2. Из Предложения 6.1
вытекает, что
![]() является несмещенной
оценкой двумерного параметра
является несмещенной
оценкой двумерного параметра
![]() .
.
Следующее свойство оценок имеет асимптотический характер и связано с увеличением
объема выборки. Для простоты рассмотрим скалярную функцию
![]() .
Предположим, что
.
Предположим, что
![]() . Рассмотрим последовательность
оценок
. Рассмотрим последовательность
оценок
![]() , соответствующих увеличивающимся
в объеме выборкам.
, соответствующих увеличивающимся
в объеме выборкам.
Вспоминая Определение 2.8 можем кратко записать, что
![]() состоятельна, если
состоятельна, если
![]() при
при
![]() .
.
Таким образом, если известно, что последовательность оценок состоятельна, то при статистической обработке данных имеет смысл увеличивать объем выборки, так как это приведет к более точному результату.
Из закона больших чисел для независимых одинаково распределенных случайных величин
(см.
![]() 5.1) вытекает, что выборочное среднее
5.1) вытекает, что выборочное среднее
![]() является состоятельной оценкой математического ожидания.
является состоятельной оценкой математического ожидания.
По Предложению 6.2 выборочная дисперсия
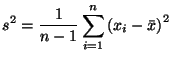
Рассмотрим еще одно полезное свойство оценок, связанное с увеличением объема
выборки:
![]() . Как и прежде,
. Как и прежде,
![]() -- последовательность оценок для скалярной функции от параметра
-- последовательность оценок для скалярной функции от параметра
![]() .
.
Последовательность оценок
![]() называется асимптотически нормальной,
если найдутся последовательность вещественных функций
называется асимптотически нормальной,
если найдутся последовательность вещественных функций
![]() и последовательность положительных функций
и последовательность положительных функций
![]() такие, что
такие, что

Последовательности
![]() и
и
![]() не определены однозначно, и далеко не всегда
не определены однозначно, и далеко не всегда
![]() совпадает
с
совпадает
с
![]() , а
, а
![]() с
с
![]() .
Понятно, что в силу центральной предельной теоремы асимптотическая нормальность
будет характерна в первую очередь для тех оценок, которые связаны с суммами
независимых одинаково распределенных слагаемых.
.
Понятно, что в силу центральной предельной теоремы асимптотическая нормальность
будет характерна в первую очередь для тех оценок, которые связаны с суммами
независимых одинаково распределенных слагаемых.
Асимптотическая нормальность является полезным свойством, так как она дает приближенное
представление о распределениях оценок при больших конечных значениях ![]() .
.
Пусть
![]() -- независимая выборка из распределения, у которого
существует дисперсия. Является ли выборочное среднее
-- независимая выборка из распределения, у которого
существует дисперсия. Является ли выборочное среднее ![]() асимптотически
нормальным ? Если да, то каковы
асимптотически
нормальным ? Если да, то каковы
![]() и
и
![]() ?
?
Сравнение оценок
Предположим, что у нас имеются две несмещенные оценки
![]() и
и
![]() для
скалярного параметра
для
скалярного параметра
![]() . Перед нами дилемма -- какую из
оценок предпочесть ? Простой и разумный совет состоит в том, чтобы выбрать
оценку с меньшей дисперсией.
. Перед нами дилемма -- какую из
оценок предпочесть ? Простой и разумный совет состоит в том, чтобы выбрать
оценку с меньшей дисперсией.
Предположим, что
![]() -- независимая выборка из равномерного
распределения в отрезке
-- независимая выборка из равномерного
распределения в отрезке
![]() , где
, где ![]() --
неизвестный параметр. Рассмотрим две следующие оценки для
--
неизвестный параметр. Рассмотрим две следующие оценки для ![]() :
:
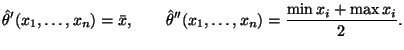

Для оценки
![]() из Примера 6.9
проверить, что
из Примера 6.9
проверить, что
![]() и вычислить
и вычислить
![]() . Указание: при нахождении дисперсии
предварительно потребуется совместная плотность случайных величин
. Указание: при нахождении дисперсии
предварительно потребуется совместная плотность случайных величин
![]() и
и
![]() .
.
С более общим подходом к сравнению оценок, основанным на рассмотрении т.н. функции
штрафа, можно ознакомиться, обратившись, например, к
![]() 4.4 книги [13]
.
4.4 книги [13]
.
|
След.: 6.6 Методы построения оценок ...
Пред.: 6.4 Выборочное среднее и ... Вверх: 6 Обзор методов математической ... |
Оглавление
Предметный указатель |