5.1 Закон больших чисел

В  2.12 произошло наше первое знакомство с законом больших чисел. Замечательно то, что утверждение закона больших чисел без изменений переносится со случая дискретных случайных величин на общий случай.

Закон Больших Чисел 1   Пусть -- последовательность независимых с.в. и выполнено условие . Тогда

Эту теорему называют еще законом больших чисел в форме Чебышева.

Следствие 5.1   Пусть -- последовательность независимых одинаково распределенных с.в. с конечной дисперсией: . Обозначим . Тогда

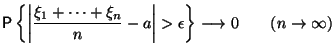
или, более кратко, при .

В действительности, это утверждение верно в более общей ситуации, а именно, предположение о существовании дисперсии не является необходимым. Имеет место так называемый закон больших чисел в форме Хинчина.

Теорема Хинчина 1  

Пусть -- последовательность независимых одинаково распределенных случайных величин, у которых существует математическое ожидание: . Тогда

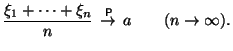
Доказательство этой теоремы можно найти в книге [4]. Там же можно ознакомиться с дальнейшими обобщениями ЗБЧ, в том числе, со знаменитым усиленным законом больших чисел, принадлежащим Колмогорову. Мы позволим себе привести небольшую цитату из этой книги, где идет речь о значении законов больших чисел: ``Через них именно теория соприкасается с практикой, именно в них заложен фундамент успехов применения теории вероятностей к различным проблемам естествознания и техники''³.