ТеорВер-Онлайн: 2.12 Закон больших чисел

2.12 Закон больших чисел

Подпункты этого параграфа:

Сходимость по вероятности

Без преувеличения можно сказать, что законы больших чисел являются одними из наиболее важных утверждений теории вероятностей.

Предложение 2.7 Пусть

-- независимы и

. Тогда

(14)

Доказательство.

Обозначим . Тогда левая часть (14) запишется в виде . Применяя второе неравенство Чебышева и Следствие 2.2, получим, что эта вероятность может быть оценена сверху следующим образом

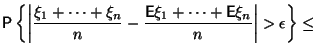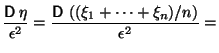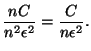Последнее выражение, очевидно, стремится к нулю при

Если все случайные величины имеют одно и то же распределение, закон больших чисел обретает следующую форму.

Следствие 2.3 Пусть

-- независимые одинаково распределенные с.в. с конечной дисперсией:

. Пусть

. Тогда

Выведем отсюда закон больших чисел для последовательности независимых испытаний Бернулли. Для этого вспомним, что число успехов может быть представлено в виде суммы независимых одинаково распределенных случайных величин с бернуллиевским распределением (см. (11) и Пример 2.7). Непосредственно получаем следующее утверждение, которое известно как теорема Бернулли.

Следствие 2.4 Пусть

-- число успехов в последовательности из

независимых испытаний Бернулли с вероятностью успеха в единичном испытании

. Тогда

Замечание 2.15

Теорема Бернулли имеет важное методологическое значение. Оно связано с возможностью ``частотного определения'' вероятности, суть которого можно объяснить следующим образом. Допустим, нас интересует вероятность некоторого случайного события , которое может произойти в результате проведения некоторого опыта. Предположим, что имеется принципиальная возможность воспроизводить неограниченное количество раз условия опыта. Если обозначить через число появлений события при независимых повторениях опыта, то согласно теореме Бернулли имеет место устойчивость частот, а именно при больших значения будут колебаться около некоторого числа, которое и есть . Этот вопрос тесно примыкает к проблеме различных подходов к определению понятия вероятности и к проблеме границ применимости теории вероятностей. Тем, кто хочет подробнее познакомиться с этими проблемами, можно порекомендовать книгу [4], где содержится их исчерпывающее обсуждение, включающее историю вопроса.