2.8 Независимость случайных величин ... 2 Дискретные случайные величины ... 2.10 Предельные теоремы для ...

2.9 Некоррелированность случайных величин

Определение 2.7   С.в. и называются некоррелированными, если

Замечание 2.8   Соотношение между независимостью и некоррелированностью случайных величин можно записать в виде следущей диаграммы:



Независимость некоррелированность
       



Прямая импликация была установлена нами в Следствии 2.1. Пример некоррелированных, но зависимых случайных величин будет приведен позже, в   4.4.

Таким образом, если ковариация отлична от нуля, то это свидетельствует о зависимости случайных величин. Для того, чтобы иметь количественный показатель того, насколько сильно зависят друг от друга случайные величины, часто используют коэффициент корреляции:

Оказывается, что всегда

Это можно доказать, применяя хорошо известное неравенство Коши-Буняковского (см. [1, Предложение 7.12]).

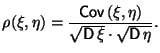
Более того, из этого неравенства вытекает, что если , то случайные величины и линейно зависимы:

Замечание 2.9  

Линейная зависимость случайных величин и или, что то же самое, их коллинеарность являются частным случаем их функциональной зависимости, то есть зависимости вида , где  -- некоторая (необязательно линейная) функция двух вещественных переменных. Из вышесказанного следует, что коэффициент корреляции хорошо отражает степень линейной зависимости между случайными величинами. Вместе с тем, позже мы покажем, что коэффициент корреляции может быть совершенно ``нечувствителен'' к функциональной зависимости (см. Замечание 4.2).

Следствие 2.2   Если независимы, то

Вытекает из п. 3) Предложения 2.2 и Следствия 2.1.

Пример 2.7   Рассмотрим вероятностное пространство , определенное формулами (2) и (3), соответствующее последовательности из независимых испытаний Бернулли. Введем случайные величины:

Можно проверить, что -- независимы и имеют бернуллиевское распределение

Число успехов в последовательности независимых испытаний (см. Пример 2.2) можно записать в виде Тогда
 
 

След.: 2.10 Предельные теоремы для ...
Пред.: 2.8 Независимость случайных величин ...
Вверх: 2 Дискретные случайные величины ... 		  Оглавление
  Предметный указатель
 

А.Д. Манита, 2001-2011