
2.2 Дискретные случайные величины
Множества вида
![]() являются событиями. Иногда для таких
событий мы будем использовать более короткое обозначение:
являются событиями. Иногда для таких
событий мы будем использовать более короткое обозначение:
![]() .
.
Так как ![]() -- не более чем счетно, то случайная величина
-- не более чем счетно, то случайная величина ![]() принимает не более чем счетное число значений:
принимает не более чем счетное число значений:
Определение 2.2
Распределением дискретной случайной величины 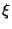 назовем таблицу:
назовем таблицу:
где
![]() .
.
Замечание 2.1
Если 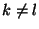 , то
, то
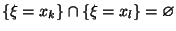 .
Более того,
.
Более того,
 Следовательно,
Следовательно,
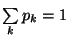 .
.
Пример 2.1
Бернуллиевской
называют случайную величину, принимающую два значения:
 Таким образом, ее распределению соответствует следующая таблица.
Таким образом, ее распределению соответствует следующая таблица.
 Таким образом, ее распределению соответствует следующая таблица.
Таким образом, ее распределению соответствует следующая таблица.
Пример 2.2
 Случайную величину
Случайную величину  естественно назвать числом успехов
в последовательности
естественно назвать числом успехов
в последовательности 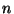 независимых испытаний Бернулли.
Найдем распределение случайной величины
независимых испытаний Бернулли.
Найдем распределение случайной величины  . Очевидно, что она
может принимать значения
. Очевидно, что она
может принимать значения
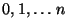 . Рассмотрим событие
. Рассмотрим событие
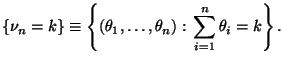 Заметим, что событие
Заметим, что событие
 состоит из
состоит из  элементарных исходов. Более того, каждый исход, входящий в событие
элементарных исходов. Более того, каждый исход, входящий в событие
 имеет одну и ту же вероятность:
имеет одну и ту же вероятность:
 Следовательно,
Следовательно,
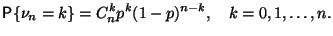 Такое распределение называется биномиальным. Запишем его в виде таблицы:
Такое распределение называется биномиальным. Запишем его в виде таблицы:
Случайная величина с биномиальным распределением.
На вероятностном пространстве Примера 1.2 определим функцию
![]() ,
принимающую на элементарном исходе
,
принимающую на элементарном исходе
![]() следующее значение:
следующее значение:

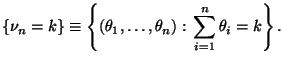
|
|
|
Пример 2.3

Будем говорить, что случайная величина ![]() имеет пуассоновское
распределение с параметром
имеет пуассоновское
распределение с параметром
![]() ,
если она принимает целые неотрицательные значения с следующими вероятностями:
,
если она принимает целые неотрицательные значения с следующими вероятностями:

|
След.: 2.3 Математическое ожидание ...
Пред.: 2.1 Счетное вероятностное пространство ... Вверх: 2 Дискретные случайные величины ... |
Оглавление
Предметный указатель |