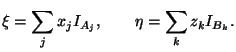2.8 Независимость случайных величин
Определим понятие независимости для дискретных случайных величин.
Определение 2.6
Случайные величины
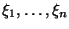 называются
независимыми, если для всех
называются
независимыми, если для всех
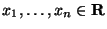
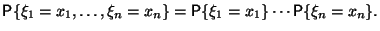 Другими словами,
Другими словами,
 набор
набор
 есть набор независимых событий.
есть набор независимых событий.
Упражнение 2.8
Показать, что события
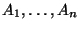 независимы
тогда и только тогда, когда случайные величины
независимы
тогда и только тогда, когда случайные величины
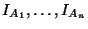 взаимно независимы.
взаимно независимы.
Предложение 2.4
Предположим, что
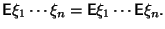
-
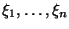 независимые случайные величины,
независимые случайные величины,
- существуют математические ожидания
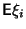 .
.
Доказательство.
Для простоты рассмотрим лишь случай ![]() .
Обозначим
.
Обозначим
![]() ,
,
![]() . Пусть
. Пусть ![]() и
и ![]() имеют следующие распределения:
имеют следующие распределения:
Обозначим
Имеют место представления
Заметим, что
Аналогично Замечанию 2.7, при любом фиксированном
Так как
![]() , если
, если
![]() ,
то мы можем воспользоваться доказанной выше Леммой 2.2:
,
то мы можем воспользоваться доказанной выше Леммой 2.2:

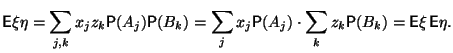
Предложение доказано. ![]()
![]()
Доказательство.
Действительно, по предложению
![]() в силу
независимости
в силу
независимости ![]() и
и ![]() . С другой стороны,
. С другой стороны,
![]() (см. Упражнение 2.7). Отсюда утверждение следствия легко следует.
(см. Упражнение 2.7). Отсюда утверждение следствия легко следует.![]()
|
След.: 2.9 Некоррелированность случайных величин ...
Пред.: 2.7 Индикаторы событий ... Вверх: 2 Дискретные случайные величины ... |
Оглавление
Предметный указатель |