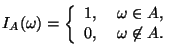2.7 Индикаторы событий
Здесь мы рассмотрим простейшие случайные величины, тесно связанные с событиями. Они очень удобны при изучении произвольных случайных величин.
Другими словами, ![]() , если происходит событие
, если происходит событие ![]() , и
, и ![]() ,
если событие
,
если событие ![]() не происходит. Таким образом,
не происходит. Таким образом, ![]() является бернуллиевской
случайной величиной (см. Пример 2.1).
является бернуллиевской
случайной величиной (см. Пример 2.1).
Предложение 2.3 (Без доказательства.)
Пусть дана последовательность
случайных величин
 такая, что все математические
ожидания
такая, что все математические
ожидания
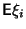 существуют и
существуют и
 Тогда
Тогда

- a)
-
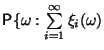 абсолютно сходится
абсолютно сходится  ,
,
- б)
- существует математическое ожидание
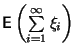 ,
,
- в)
-
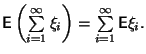
Лемма 2.2
Пусть
 --
последовательность несовместных событий:
--
последовательность несовместных событий:
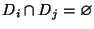 . Рассмотрим
случайную величину вида
. Рассмотрим
случайную величину вида
Предположим, что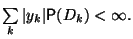 Тогда
Тогда

Предположим, что
Доказательство.
Данное утверждение есть следствие сформулированного выше Предложения.
Действительно, обозначим
![]() . Заметим, что
. Заметим, что
![]() .
Легко проверить, что условия Предложения 2.3 выполнены. Следовательно,
.
Легко проверить, что условия Предложения 2.3 выполнены. Следовательно,

Замечание 2.7
Обратим внимание на то, что в бесконечной сумме (8) при любом
фиксированном ![]() только одно слагаемое отлично от нуля. Это вытекает
из несовместности событий
только одно слагаемое отлично от нуля. Это вытекает
из несовместности событий ![]() .
.
|
След.: 2.8 Независимость случайных величин ...
Пред.: 2.6 Общие свойства дисперсии ... Вверх: 2 Дискретные случайные величины ... |
Оглавление
Предметный указатель |