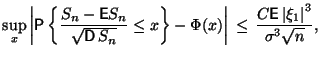ТеорВер-Онлайн: 5.2 Центральная предельная теорема

Интегральная предельная теорема Муавра-Лапласа, которая обсуждалась в

2.10, интересна тем, что она является частным случаем общей и универсальной центральной предельной теоремы. Основополагающий вклад в разработку этой тематики внесли выдающиеся отечественные математики: П.Л. Чебышев, А.А. Марков и А.М. Ляпунов.

Мы приведем без доказательства вариант ЦПТ для независимых одинаково распределенных слагаемых.

Центральная Предельная Теорема 1 Пусть

-- последовательность независимых одинаково распределенных с.в. с конечной дисперсией. Обозначим

. Тогда

где

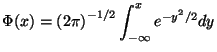-- функция распределения стандартного нормального закона.

Замечание 5.1 Обозначим

. Тогда

. Следовательно, утверждение ЦПТ может быть записано в виде

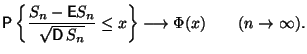
Мы не приводим здесь доказательства центральной предельной теоремы, так как оно требует привлечения дополнительного математического аппарата, который в нашем дальнейшем изложении не потребуется. Доказательство ЦПТ можно найти во многих учебниках [4,12,14].

Как уже отмечалось выше, интегральную теорему Муавра-Лапласа для схемы Бернулли можно считать следствием ЦПТ.

Замечание 5.2

Существуют обобщения ЦПТ на случай независимых разнораспределенных слагаемых. При этом, на отдельные слагаемые накладываются условия, обеспечивающие их ``пренебрежимо малый'' вклад в сумму с ростом . Наиболее известными условиями такого рода являются условия Ляпунова и Линдеберга.

ЦПТ имеет огромное значение для применений теории вероятностей в естествознании и технике. Ее действие проявляется там, где наблюдаемый процесс подвержен влиянию большого числа независимых случайных факторов, каждый из которых лишь ничтожно мало изменяет течение процесса. Наблюдатель, следящий за состоянием процесса в целом, наблюдает лишь суммарное действие этих факторов. Эта схема поясняет также исключительное место, которое нормальное распределение занимает среди другий вероятностных распределений.

ЦПТ дает возможность аппроксимировать распределение сумм независимых с.в. нормальным распределением, чем часто пользуются на практике. В связи с этим, очень важным является вопрос о том, насколько быстро допредельное выражение в ЦПТ приближается к

. Приведем формулировку теоремы Бэрри-Эссеена о скорости сходимости в ЦПТ⁴. Предположим, что выполнены условия ЦПТ для независимых одинаково распределенных с.в., и, кроме того, существует . Тогда справедлива оценка