
5.3 Одномерное случайное блуждание
Рассмотрим последовательность независимых одинаково распределенных
случайных величин
![]() с распределением
с распределением
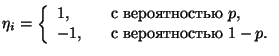
Введем последовательность случайных величин
Последовательность
![]() назовем случайным
блужданием на множестве
назовем случайным
блужданием на множестве
![]() , выходящим из точки
, выходящим из точки ![]() . Параметр
. Параметр
![]() интерпретируется как дискретное время, случайная величина
интерпретируется как дискретное время, случайная величина ![]() -- как положение (координата) блуждающей частицы в момент времени
-- как положение (координата) блуждающей частицы в момент времени ![]() .
.
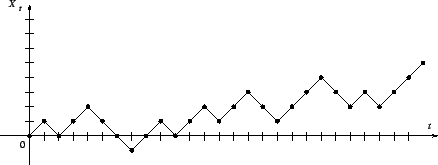
Наша цель -- дать качественное описание ![]() при больших
при больших ![]() .
Рассмотрим на вещественной прямой интервалы вида
.
Рассмотрим на вещественной прямой интервалы вида
![]() ,
где
,
где
![]() .
.
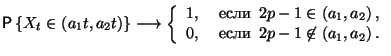
Доказательство.
Это утверждение следует из закона больших чисел.
Предположим, что
![]() . Достаточно
выбрать
. Достаточно
выбрать
![]() таким, что
таким, что
![]() ,
и применить ЗБЧ.
,
и применить ЗБЧ. ![]()
Следовательно, при больших ![]() распределение случайной величины
распределение случайной величины ![]() ,
главным образом, сосредоточено в внутри сколь угодно ``узкого'' конуса
,
главным образом, сосредоточено в внутри сколь угодно ``узкого'' конуса
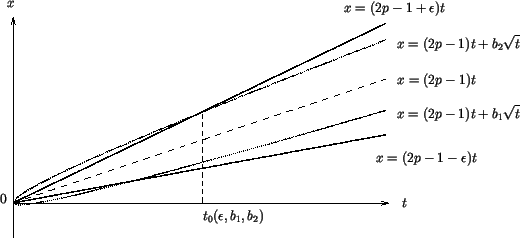
Можно показать, что при любых фиксированных
![]() ,
, ![]() и
и ![]() найдется такое
найдется такое
![]() , что
при
, что
при ![]()

Доказательство.
Вытекает из центральной предельной теоремы.![]()