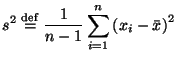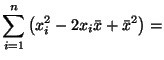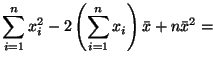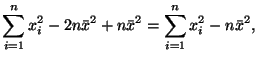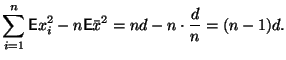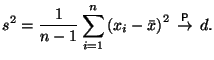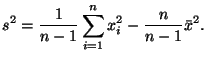6.4 Выборочное среднее и выборочная дисперсия
Иногда исследователь ставит перед собой более конкретную проблему: как, основываясь на выборке, оценить интересующие его числовые характеристики неизвестного распределения, не прибегая к приближению этого распределения как такового, то есть без построения выборочных функций распределения, гистограмм и т.п.
В данном параграфе мы обсудим простые (но, как увидим в дальнейшем, весьма хорошие)
выборочные аппроксимации для математического ожидания и дисперсии. Замечательно
то, что они применимы в очень общей ситуации. Мы будем предполагать, что независимая
выборка
![]() взята из неизвестного распределения,
у которого существует математическое ожидание и дисперсия (обозначим эти неизвестные
значения через
взята из неизвестного распределения,
у которого существует математическое ожидание и дисперсия (обозначим эти неизвестные
значения через ![]() и
и ![]() соответственно).
соответственно).
Величины, вычисляемые по выборке,
и
называются выборочным средним и выборочной дисперсией.
Следует особо подчеркнуть, что определенные выше величины зависят только от
выборки. Следующее предложение объясняет, почему естественно считать ![]() выборочным аналогом математического ожидания, а
выборочным аналогом математического ожидания, а ![]() -- выборочным
аналогом дисперсии.
-- выборочным
аналогом дисперсии.
Математические ожидания ![]() и
и ![]() совпадают
с оцениваемыми неизвестными величинами:
совпадают
с оцениваемыми неизвестными величинами:
Дисперсия
Доказательство.
Используя линейность математического ожидания, получим

Так как выборка независимая, то
![]() .
Следовательно,
.
Следовательно,
![]() при
при
![]() .
.
Покажем теперь, что
![]() . Первое замечание состоит в том, что
. Первое замечание состоит в том, что
![]() не зависит от сдвига всех элементов выборки на одну и ту же константу,
то есть, значения выражения (30) для выборок
не зависит от сдвига всех элементов выборки на одну и ту же константу,
то есть, значения выражения (30) для выборок
![]() и
и
![]() одинаковы. Поэтому без ограничения общности
мы будем считать, что
одинаковы. Поэтому без ограничения общности
мы будем считать, что
![]() . При этом предположении
. При этом предположении
![]()
Это утверждение свидетельствует о том, что ![]() и
и ![]() являются
``качественными приближениями'' для неизвестных величин
являются
``качественными приближениями'' для неизвестных величин ![]() и
и ![]() .
Свойство (31) называется несмещенностью.
Тот факт, что дисперсия
.
Свойство (31) называется несмещенностью.
Тот факт, что дисперсия ![]() исчезает с увеличением объема выборки
дает основание для вывода о том, что, чем больше данных измерений мы возьмем
для статистической обработки, тем точнее будут наши выводы.
исчезает с увеличением объема выборки
дает основание для вывода о том, что, чем больше данных измерений мы возьмем
для статистической обработки, тем точнее будут наши выводы.
Для оценивания дисперсии по выборке может быть использована также функция

Доказательство.
Как и при доказательстве Предложения 6.1 без ограничения общности
будем считать, что
![]() . При этом предположении
. При этом предположении
![]() .
Из (32) вытекает, что
.
Из (32) вытекает, что
Применяя закон больших чисел в форме Хинчина к последовательности
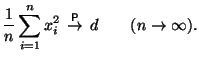
![]()
Здесь мы воспроизводим замечание о вычислениях, приведенное в [12, с. 116].
Из соотношения (33) вытекает следующее представление для ![]() :
:
Математически формулы (30) и (34) дают одно и то же значение. Но, если нам необходимо вручную вычислить выборочную дисперсию, то следует это делать только по формуле (30), так как вычисления по формуле (34) потребовали бы учета намного большего числа значащих цифр, чем в случае применения формулы (30).
Имеется большое число практически важных приемов, призванных облегчить вычислительную работу с конкретными числовыми выборками. Для знакомства с ними рекомендуем читателю обратиться к книге [11].
В настоящее время существует много прикладных компьютерных программ, которые можно и нужно использовать для обработки числовых данных. С некоторыми наиболее популярными специализированными статистическими пакетами (Stadia, StatGraphics) можно познакомиться по книге [13], к которой также приводится их сравнение. Для статистической обработки небольших массивов данных вполне подойдет любой хороший универсальный математический пакет (Mathematica, Maple, Matlab).
Вычислим выборочное среднее и выборочную дисперсию для числовых данных Примера 6.4
на странице ![[*]](crossref.png) . Подставив данные в формулы (29)
и (30), найдем для выборки
. Подставив данные в формулы (29)
и (30), найдем для выборки
![]()
|
След.: 6.5 Оценивание неизвестных параметров ...
Пред.: 6.3 Гистограмма ... Вверх: 6 Обзор методов математической ... |
Оглавление
Предметный указатель |