
6.1 Понятие о выборке
Отправной точкой любого статистического анализа являются данные, полученные
экспериментатором в результате опыта. Допустим, что опыт состоял из ![]() повторных измерений некоторой неизвестной величины и в результате получены
значения
повторных измерений некоторой неизвестной величины и в результате получены
значения
![]() . Эти значения естественно считать реализацией
набора из
. Эти значения естественно считать реализацией
набора из ![]() независимых одинаково распределенных случайных величин с
неизвестной функцией распределения
независимых одинаково распределенных случайных величин с
неизвестной функцией распределения ![]() . Вектор данных
. Вектор данных
Часто встречается ситуация, когда экспериментатор имеет основания предполагать,
что неизвестное распределение принадлежит некоторому семейству распределений
![]() , зависящему от параметра
, зависящему от параметра
![]() .
В этом случае проблема статистического анализа сводится к получению информации
об этом неизвестном параметре. Проиллюстрируем все вышесказанное следующими
примерами.
.
В этом случае проблема статистического анализа сводится к получению информации
об этом неизвестном параметре. Проиллюстрируем все вышесказанное следующими
примерами.
Неизвестная величина ![]() измеряется некоторым несовершенным прибором,
прибавляющим к
измеряется некоторым несовершенным прибором,
прибавляющим к ![]() случайную ошибку, распределенную по нормальному закону
с нулевым средним и известной дисперсией
случайную ошибку, распределенную по нормальному закону
с нулевым средним и известной дисперсией
![]() . Если измерения
проводятся
. Если измерения
проводятся ![]() раз, то в итоге мы имеем независимую выборку
раз, то в итоге мы имеем независимую выборку
![]() из распределения, принадлежащему семейству
из распределения, принадлежащему семейству
![]() .
Об этой статистической модели принято говорить как о независимой выборке из
нормального распределения с известной дисперсией.
.
Об этой статистической модели принято говорить как о независимой выборке из
нормального распределения с известной дисперсией.
Если в ситуации предыдущего примера документация прибора ничего не сообщает
о дисперсии совершаемой им ошибки, то мы имеем дело с независимой выборкой
![]() из распределения, принадлежащему семейству
из распределения, принадлежащему семейству
![]() ,
,
![]() . То есть, в такой постановке неизвестный
параметр
. То есть, в такой постановке неизвестный
параметр ![]() двумерен.
двумерен.
Если исследователь не уверен в том, что ошибка измерительного прибора
является нормальной случайной величиной, он вправе поставить перед собой следующий
вопрос: как, основываясь на полученной им независимой выборке
![]() из неизвестного распределения с функцией распределения
из неизвестного распределения с функцией распределения ![]() , проверить
гипотезу о принадлежности
, проверить
гипотезу о принадлежности ![]() классу нормальных распределений.
классу нормальных распределений.
Большим источником статистических данных является аналитическая химия. Рассмотрим
числовые данные, взятые из книги [5, с. 41]: для контроля качества
в 40 пробах стали GS50 определялось содержание углерода ![]() (%С) и
прочность на разрыв
(%С) и
прочность на разрыв ![]() (Н/мм
(Н/мм![]() ). Данные оформлены в виде таблицы
чисел:
). Данные оформлены в виде таблицы
чисел:
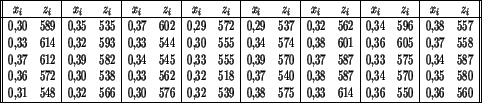
Таким образом, мы имеем дело с независимой выборкой
![]() :
:
|
0.3, 0.33, 0.37, 0.36, 0.31, 0.29, 0.34, 0.39,
0.37, 0.38, 0.35, 0.32, 0.39, 0.3, 0.32, 0.32,
0.38, 0.37, 0.38, 0.33, 0.37, 0.33, 0.34, 0.33, 0.3, 0.34, 0.36,
0.33, 0.34, 0.36, 0.29, 0.3, 0.33, 0.32, 0.32, 0.38, 0.37, 0.34,
0.35, 0.36,
|
имеющей объем 40 и составленной из данных измерений содержания углерода,
и с независимой выборкой
![]() :
:
|
589, 614, 612, 572, 548, 537, 574, 570, 540, 575,
535, 593, 582, 538, 566, 562, 601, 587, 587,
614, 602, 544, 545, 562, 576, 596, 605, 575, 570, 550, 572, 555, 555,
518, 539, 557, 558, 587, 580, 560,
|
составленную из измерений прочности на разрыв. В дальнейшем для иллюстрации вводимых понятий мы будем многократно возвращаться к этому числовому примеру.
|
След.: 6.2 Эмпирическая функция распределения ...
Пред.: 6 Обзор методов математической ... Вверх: 6 Обзор методов математической ... |
Оглавление
Предметный указатель |