
6.3 Гистограмма
Помимо эмпирических функций распределения, наглядное (но,
вместе с тем, довольно приближенное) представление о неизвестном распределении
можно получить при помощи гистограмм. Пусть
![]() -- независимая выборка из неизвестного распределения
-- независимая выборка из неизвестного распределения ![]() . Выберем два
числа
. Выберем два
числа ![]() и
и ![]() ,
,
![]() , такими, чтобы все числа
, такими, чтобы все числа
![]() попали внутрь интервала
попали внутрь интервала ![]() . Разобъем этот интервал на
конечное число меньших интервалов:
. Разобъем этот интервал на
конечное число меньших интервалов:

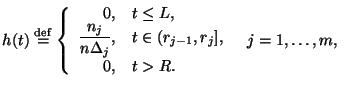
Таким образом, гистограмма представляет собой график кусочно-постоянной
функции, такой, что площадь столбца с основанием, например,
![]() равна частоте попадания измерений в этот интервал группировки. Вспоминая материал
равна частоте попадания измерений в этот интервал группировки. Вспоминая материал
![]() 3.4,
можно заключить, что гистограмма является выборочным аналогом плотности распределения.
3.4,
можно заключить, что гистограмма является выборочным аналогом плотности распределения.
При построении гистограмм мы имеем свободу в выборе интервала ![]() ,
числа интервалов разбиения
,
числа интервалов разбиения ![]() и самих точек
и самих точек
![]() .
Для получения хороших приближений для плотности неизвестного распределения следует
всякий раз учитывать специфику конкретных данных. Самые общие рекомендации по
выбору этих параметров таковы.
.
Для получения хороших приближений для плотности неизвестного распределения следует
всякий раз учитывать специфику конкретных данных. Самые общие рекомендации по
выбору этих параметров таковы.
- Значение
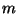 должно быть существенно меньше, чем объем выборки
должно быть существенно меньше, чем объем выборки 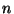 ,
но вместе с тем не слишком малым, чтобы гистограмма имела достаточно подробный
профиль.
,
но вместе с тем не слишком малым, чтобы гистограмма имела достаточно подробный
профиль.
- Интервалы разбиения следует выбирать так, чтобы каждый из них содержал ``достаточно много'' элементов выборки. Если в группах недостаточно большое число данных, то возможные случайные флуктуации их числа приводят к значительным искажениям реальной картины.