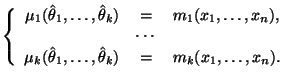6.5 Оценивание неизвестных параметров ... 6 Обзор методов математической ... 7 Метод наименьших квадратов ...

6.6 Методы построения оценок

Подпункты этого параграфа:

Метод моментов

Идея этого метода заключается в приравнивании теоретических и эмпирических моментов. Поэтому мы начнем с обсуждения этих понятий.

Пусть -- независимая выборка из распределения , зависящего от неизвестного параметра Теоретическим моментом -го порядка называется функция

где -- случайная величина с функцией распределения . Особо отметим, что теоретический момент есть функция от неизвестных параметров, коль скоро распределение зависит от этих параметров. Будем считать, что математические ожидания существуют, по крайней мере, для .

Эмпирическим моментом -го порядка называется

Отметим, что по своему определению эмпирические моменты являются функциями от выборки. Заметим, что -- это хорошо нам известное выборочное среднее.

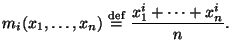
Для того, чтобы найти оценки неизвестных параметров по методу моментов следует:

  1. явно вычислить теоретические моменты 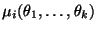, , 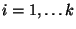и составить следующую систему уравнений для неизвестных переменных :

    (35)

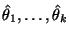    В этой системе рассматриваются как фиксированные параметры.
  2. решить систему (35) относительно переменных 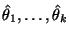. Так как правая часть системы зависит от выборки, то в результате 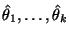окажутся функциями от :

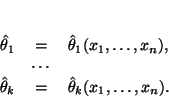
    \begin{displaymath} % latex2html id marker 21881\begin{array}{rcl} \hat{\theta... ...} & = & \hat{\theta }_{k}(x _{1 },\ldots ,x _{n }). \end{array}\end{displaymath}

    Это и есть искомые оценки параметров по методу моментов.

Замечание 6.7  

В общей ситуации вопрос о разрешимости (вообще говоря, нелинейной) системы (35) не является простым. Он близок хорошо известной в анализе задаче о неявной функции. Мы не приводим здесь никаких теорем, гарантирующих существование решения и его единственность, так как в этом нет большого практического смысла для статистических приложений. Дело в том, что в большом числе важных статистических моделей, соответствующих основным вероятностным распределениям, эта система без труда решается в каждом конкретном случае. При этом оказывается, что оценки, получаемые по методу моментов, оказываются состоятельными (см. Определение 6.4).

Метод наибольшего правдоподобия

Пусть, как и прежде, -- независимая выборка из распределения с функцией распределения , зависящей от неизвестного параметра Определим функцию правдоподобия, полагая

если -- абсолютно непрерывна и имеет плотность , либо

если есть функция распределения некоторой дискретной случайной величины , причем .

Переменные следует считать основными для функции , а -- дополнительными параметрами. Считая фиксированными, найдем точку , в которой функция правдоподобия принимает наибольшее значение. Понятно, что эта точка будет зависеть от заранее фиксированной выборки , следовательно, мы получим набор функций от выборки:

(36)

что и будет искомой оценкой по методу наибольшего правдоподобия.

Сформулируем вышесказанное в виде формального определения.

Определение 6.6  

Функция от выборки (36) называется оценкой наибольшего правдоподобия (о.н.п.), если

Замечание 6.8  

Если функция правдоподобия является дифференцируемой по переменным , то о.н.п.  удовлетворяет следующей системе уравнений:

Это хорошо известные из курса математического анализа необходимые условия экстремума функции нескольких переменных.

Пример 6.10  

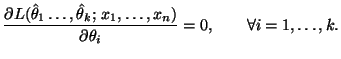
Рассмотрим статистическую модель нормальной выборки из Примера 6.2. Обозначим , . Будем искать точку, в которой достигается максимум функции правдоподобия:

Очевидно, что максимум достигается в той же точке, что и у функции . Чтобы найти ее точки экстремума, приравняем к нулю частные производные:
 
 

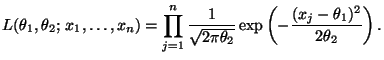
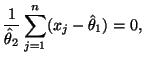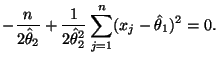Эта система имеет единственное решение 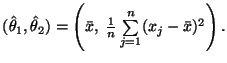Теперь следует обосновать, что это действительно точка глобального максимума. Это упражнение оставляется читателю для самостоятельного решения.

Оценки максимального правдоподобия широко применяются. Во многих регулярных (т.е., хороших) ситуациях они оказываются состоятельными и асимптотически нормальными.

Отметим, что далеко не всегда функцию правдоподобия можно считать гладкой. В этом случае, изложенная выше схема бесполезна, но, тем не менее, задача не является безнадежной. Проиллюстрируем это примером.

Пример 6.11  

Рассмотрим независимую выборку из равномерного распределения в отрезке , где -- неизвестный параметр. Выпишем функцию правдоподобия

и перепишем ее в более удобном виде:

Легко видеть, что максимальное значение эта функция принимает в точке . Это и есть искомая оценка наибольшего правдоподобия для параметра .

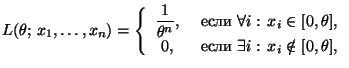
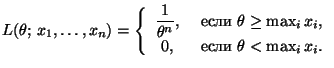
След.: 7 Метод наименьших квадратов ...
Пред.: 6.5 Оценивание неизвестных параметров ...
Вверх: 6 Обзор методов математической ... 		  Оглавление
  Предметный указатель
 

А.Д. Манита, 2001-2011