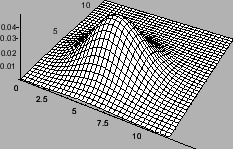
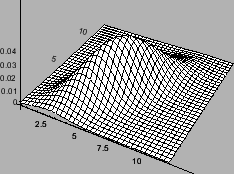
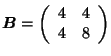4.6 Многомерное нормальное распределение
Важнейшим примером совместного распределения нескольких случайных величин является многомерное нормальное распределение. Оно играет важную роль в теории вероятностей и часто возникает в различных статистических задачах.
Говорят, что набор случайных величин
![]() имеет многомерное
нормальное распределение, если
найдутся вещественный вектор
имеет многомерное
нормальное распределение, если
найдутся вещественный вектор
![]() , невырожденная вещественная
, невырожденная вещественная
![]() -матрица
-матрица
![]() и набор независимых стандартных
нормальных случайных величин
и набор независимых стандартных
нормальных случайных величин
![]() такие, что
такие, что
Для многомерного нормального распределения часто употребляют синонимичное название многомерное гауссовское распределение.
Соотношения (26) записываются более компактно, если воспользоваться
матричной формой:
![]() .
.
Справедливы следующие утверждения.
- С.в.
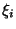 имеет нормальное распределения
имеет нормальное распределения
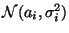 ,
где
,
где
 .
.
-
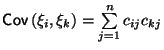 .
.
Доказательство.
То, что ![]() имеет нормальный закон распределения, вытекает из Упражнения 4.7
и предположения о том, что
имеет нормальный закон распределения, вытекает из Упражнения 4.7
и предположения о том, что
![]() независимые
независимые
![]() случайные величины. Используя линейность математического ожидания, находим,
что
случайные величины. Используя линейность математического ожидания, находим,
что
![]() . По Следствию 4.4
. По Следствию 4.4
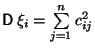 .
Чтобы доказать второе утверждение, применим свойство билинейности ковариации
(см. Замечание 2.4):
.
Чтобы доказать второе утверждение, применим свойство билинейности ковариации
(см. Замечание 2.4):
 |
|||
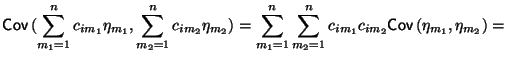 |
|||
 |
|||
Мы воспользовались тем, что
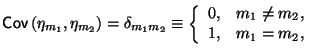 в силу предположения о независимости набора
в силу предположения о независимости набора
![]()
Рассмотрим ![]() -матрицу
-матрицу
![]() , где
, где
![]() -- матрица транспонированная к
-- матрица транспонированная к ![]() . Легко видеть, что такая матрица симметрична
(
. Легко видеть, что такая матрица симметрична
(
![]() ) и является невырожденной в силу невырожденности матрицы
) и является невырожденной в силу невырожденности матрицы ![]() .
Более того, из только что доказанного Предложения следует, что
.
Более того, из только что доказанного Предложения следует, что
![]() .
.
Доказать, что матрица ![]() является строго положительной в следующем
смысле: для любого ненулевого вещественного вектора
является строго положительной в следующем
смысле: для любого ненулевого вещественного вектора
![]()

Матрицу
![]() принято называть матрицей ковариаций, а
вектор
принято называть матрицей ковариаций, а
вектор
![]() -- вектором средних многомерного
нормального распределения. Оказывается, что этих двух характеристик достаточно
для того, чтобы полностью описать многомерное нормальное распределение. А именно,
имеет место следующее утверждение.
-- вектором средних многомерного
нормального распределения. Оказывается, что этих двух характеристик достаточно
для того, чтобы полностью описать многомерное нормальное распределение. А именно,
имеет место следующее утверждение.
Плотность многомерного нормального распределения записывается в виде следующей формулы:
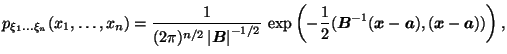

Если ![]() , то функция, выписанная в Предложении, принимает вид обычной
нормальной плотности (см. стр.
, то функция, выписанная в Предложении, принимает вид обычной
нормальной плотности (см. стр. ![[*]](crossref.png) ).
).
Доказательство.
Воспользуемся формулой вероятности попадания в область (Следствие 4.1)
и сделаем замену переменных в интеграле:
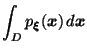 |
|||
 замена замена |
|||
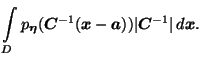 |
Поскольку это верно для любой области
![]() , то равны и подинтегральные
функции
, то равны и подинтегральные
функции
Так как
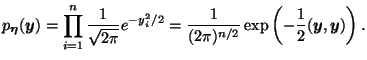
![]()
Из вида многомерной нормальной плотности видно, что в нем участвуют лишь параметры
![]() и
и ![]() . Поэтому этот закон распределения часто обозначают
. Поэтому этот закон распределения часто обозначают
![]() .
.
Утверждение Предложения 4.7 можно считать эквивалентным
определением многомерного нормального распределения. Если плотность имеет указанный
вид с некоторой невырожденной положительной матрицей ![]() , то существуют
такие
, то существуют
такие ![]() ,
, ![]() и
и
![]() , что справедливо представление (26).
, что справедливо представление (26).
Сформулируем без доказательства одно важное предложение.
Предположим, что вектор
![]() имеет многомерное нормальное
распределение. Тогда любой набор его компонент
имеет многомерное нормальное
распределение. Тогда любой набор его компонент
![]() имеет (
имеет (![]() -мерное) нормальное распределение.
-мерное) нормальное распределение.
Показать, что если какие-то из компонент нормального вектора некоррелированы, то они независимы.
Чему равны дисперсии компонент двумерного случайного вектора и коэффициент корреляции между ними для каждого из двух примеров Замечания 4.5 ?
Иногда матрица ![]() , участвующая в соотношениях (26),
имеет ранг меньший
, участвующая в соотношениях (26),
имеет ранг меньший ![]() . В этом случае говорят, что
. В этом случае говорят, что
![]() имеет вырожденное многомерное нормальное распределение. У такого распределения
плотность не существует.
имеет вырожденное многомерное нормальное распределение. У такого распределения
плотность не существует.
|
След.: 5 Предельные законы теории ...
Пред.: 4.5 Формула свертки ... Вверх: 4 Совместное распределение общих ... |
Оглавление
Предметный указатель |