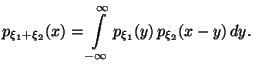4.5 Формула свертки
Многие важные случайные величины представляются в виде сумм независимых слагаемых. Нижеследующее утверждение устанавливает, как распределение суммы связано с распределениями слагаемых.
Доказательство.
Пусть
![]() .
.
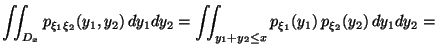 |
|||
 |
Так как это равенство выполнено при всех ![]() , то из определения плотности
распределения получаем формулу свертки (25).
, то из определения плотности
распределения получаем формулу свертки (25). ![]()
Замечание 4.3
Если 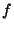 и
и  -- абсолютно интегрируемые функции
на
-- абсолютно интегрируемые функции
на
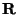 , то определена операция свертки функций
, то определена операция свертки функций
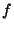 и
и  :
:
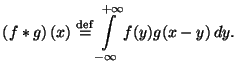 Таким образом, доказанное выше Предложение гласит, что если
Таким образом, доказанное выше Предложение гласит, что если 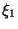 и
и 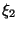 независимые с.в., имеющие плотность, то
независимые с.в., имеющие плотность, то
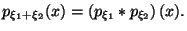
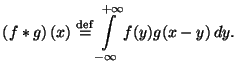
Упражнение 4.5
Проверить свойства коммутативности и ассоциативности свертки:
-
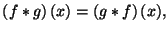
-
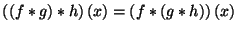 .
.
Замечание 4.4
Предложение может быть обобщено на случай произвольного числа
независимых слагаемых: если
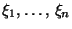 -- независимые
с.в., имеющие плотность, то
-- независимые
с.в., имеющие плотность, то



Упражнение 4.7
Из Упражнений 3.6 и 4.6 вывести следующую теорему: сумма произвольного числа независимых нормальных случайных величин имеет нормальное распределение. Указание: сначала доказать это утверждение для двух случайных величин, затем -- по индукции.
|
След.: 4.6 Многомерное нормальное распределение ...
Пред.: 4.4 О некоррелированных зависимых ... Вверх: 4 Совместное распределение общих ... |
Оглавление
Предметный указатель |