4.3 Независимость случайных величин

Следующее определение обобщает понятие независимости, данное в  2.8, на случай произвольных случайных величин.

Определение 4.3   Случайные величины называются независимыми, если

Следствие 4.3   Случайные величины 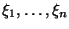с абсолютно непрерывным распределением являются независимыми тогда и только тогда, когда

Предложение 4.3   Есл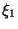и и 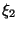независимы, то для любой пары интервалов 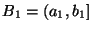и

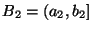
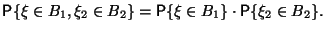
Доказательство.

При доказательстве поочередно пользуемся Определениями 4.1, 4.3 и 3.5:

Замечание 4.1   Такое же утверждение имеет место для любого конечного числа случайных величин

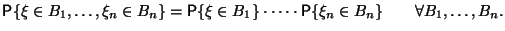
Предложение 4.4   Если 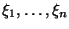-- независимые абсолютно непрерывные случайные величины, у которых существует математическое ожидание, то

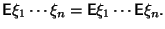
Доказательство.

Доказательство просто -- последовательно применяем Предложение 4.2, Следствие 4.3 и определение (17):

Следствие 4.4   Если -- независимы, то

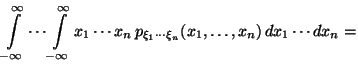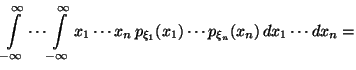Доказательство. Достаточно показать, что (). Это, в свою очередь, следует из Предложения 4.4.