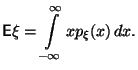3.5 Математическое ожидание и дисперсия абсолютно непрерывной случайной величины
Определение 3.8
Математическим ожиданием
случайной величины 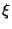 с плотностью
с плотностью
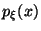 назовем число
назовем число
По определению математическое ожидание существует тогда и только тогда, когда интеграл сходится абсолютно.
По определению математическое ожидание существует тогда и только тогда, когда интеграл сходится абсолютно.
Формула (17) аналогична формуле (7) для дискретных случайных величин.
Предложение 3.2 (Без доказательства.)
Пусть
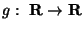 -- некоторая функция. Имеет место формула
-- некоторая функция. Имеет место формула
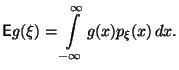 Математическое ожидание
Математическое ожидание
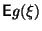 существует тогда и только тогда,
когда этот интеграл сходится абсолютно.
существует тогда и только тогда,
когда этот интеграл сходится абсолютно.
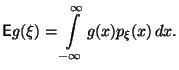
В частности,
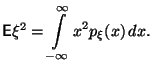 Теперь понятно, как вычислять дисперсию
Теперь понятно, как вычислять дисперсию
![]() .
.
Упражнение 3.8
Вычислить математическое ожидание и дисперсию равномерного
и показательного распределений (см. определения в
 3.4).
3.4).
Упражнение 3.9
Доказать, что для случайной
величины 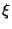 , распределенной по нормальному закону
, распределенной по нормальному закону
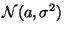 ,
,
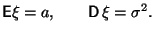 Указание: при доказательстве целесообразно вначале воспользоваться результатом
Упражнения 3.6 и свести задачу к проверке того, что
для случайной величины
Указание: при доказательстве целесообразно вначале воспользоваться результатом
Упражнения 3.6 и свести задачу к проверке того, что
для случайной величины 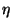 со стандартным нормальным распределением
со стандартным нормальным распределением
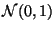
 При проверке этого факта удобно применить результат Упражнения 3.5.
При проверке этого факта удобно применить результат Упражнения 3.5.