
4.1 Совместная функция распределения, плотность
Как и раньше, наиболее универсальным инструментом являются функции распределения.
Определение 4.1
Совместной функцией распределения
случайных величин
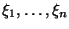 , назовем функцию
, назовем функцию
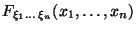 ,
зависящую от
,
зависящую от 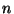 вещественных переменных, такую, что
вещественных переменных, такую, что
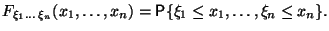
Предложение 4.1 (Без доказательства)
. Перечислим некоторые свойства функций
распределения нескольких случайных величин:
-
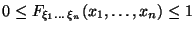 ;
;
- Монотонность по каждой переменной, например,
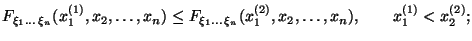
- Пределы на ``минус бесконечности'': если в совместной функции распределения
зафиксировать все переменные, кроме одной, а оставшуюся переменную устремить
к
 , то предел равен нулю. Например, для фиксированных
, то предел равен нулю. Например, для фиксированных
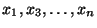
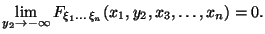
- Пределы на ``плюс бесконечности''. Если все переменные устремить к
 ,
в пределе получится единица:
Если зафиксируем все переменные, кроме одной, которую устремим к
,
в пределе получится единица:
Если зафиксируем все переменные, кроме одной, которую устремим к
 ,
получим функцию распределения меньшего набора случайных величин. Например,
,
получим функцию распределения меньшего набора случайных величин. Например,
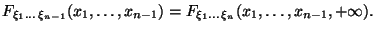
Упражнение 4.1

Вывести из этого предложения, что

Наиболее удобный для теории и очень важный для практических приложений случай -- это случай абсолютно непрерывных распределений.
Определение 4.2
Распределение
случайныx величин
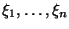 называется абсолютно непрерывным,
если существует функция
называется абсолютно непрерывным,
если существует функция
 такая, что
такая, что
 , обладающая
вышеперечисленными свойствами, называется совместной плотностью распределения
набора случайных величин
, обладающая
вышеперечисленными свойствами, называется совместной плотностью распределения
набора случайных величин
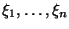 .
.
-
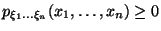 ,
,
-
 ,
,
-

Это очень полезная формула, она носит название формулы вероятности попадания в область. Она расширяет формулу (23), которая является ее частным случаем для областей вида
Следствие 4.2
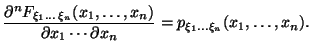
В тех точках
![]() , в которых плотность
, в которых плотность
![]() непрерывна, верна формула
непрерывна, верна формула
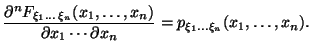
Упражнение 4.2
Показать, что


|
След.: 4.2 Математическое ожидание функции ...
Пред.: 4 Совместное распределение общих ... Вверх: 4 Совместное распределение общих ... |
Оглавление
Предметный указатель |

