9.3 Критерий согласия для ... 9 Статистические гипотезы ... 9.5 Проверка нормальности при ...

9.4 О критериях согласия Колмогорова и Смирнова

Часто при проверке гипотез о распределении тех или иных данных недостаточно применить какой-то один критерий, в особенности, когда данные наблюдений не показывают значимого отклонения от гипотезы, и ситуация представляется сомнительной. В этих случаях целесообразно воспользоваться другими критериями, основанными на других вероятностных идеях, чтобы при их помощи подвергнуть анализу те же данные. Таким образом, очень важно иметь широкий арсенал методов для статистической обработки данных.

В настоящем параграфе мы кратко опишем два других эффективных подхода, приводящих к хорошим критериям согласия. Критерий Пирсона, изложенный в   9.2 и   9.3, может применяться в самой общей ситуации, являясь весьма универсальным. Его применение особенно оправдано в случае выборок из дискретных распределений. Однако для ряда статистических моделей выводы этого критерия могут быть недостаточно эффективными.

Критерии Колмогорова и Смирнова, о которых идет речь ниже, очень широко применяются в случае непрерывных функций распределения.

Мы ограничимся лишь рассмотрением случая простой гипотезы

Основой всех методов является рассмотрение некоторой удачно выбранной меры расхождения между выборкой и гипотетическим распределением, а также возможность описать асимптотическое распределение этой меры расхождения при росте объема выборки. В случае критерия Пирсона этой мерой расхождения была функция .

Для критериев Колмогорова и Смирнова выбор меры расхождения связан с эмпирической функцией распределения  (см. Определение 6.1). А именно, рассматривается статистика Колмогорова

и статистика Смирнова

соответственно. Замечательно то, что эти функции легко могут быть вычислены по выборке (не требуется брать какие-либо интегралы, все сводится к простым выражениям, содержащим конечное суммирование и взятие максимума, см., например,  10.2 в [13]).

Коснемся вопроса об асимптотическом распределении этих функций. По теореме Гливенко (см. (28)) при выполнении гипотезы  статистика  стремится к нулю при . Оказывается, что если ее домножить на , то в пределе получится нетривиальное распределение. Более точно, верна теорема Колмогорова: Если гипотеза  верна и непрерывна, то

  1. распределение статистики 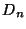является одним и тем же для любой функции распределения 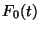и
  2. у последовательности 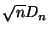существует предельное распределение при .
Это предельное распределение не совпадает ни с одним упоминавшемся здесь ранее и носит название распределения Колмогорова.

Аналогичное по характеру утверждение имеет место и для статистики Смирнова, а именно, при верной гипотезе  и непрерывной 

  1. распределение 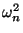зависит только от 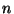и не зависит от ,
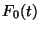  2. у последовательности 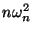существует предельное распределение при .
Теоремы Колмогорова и Смирнова являются основой для построения соответствующих критериев согласия с критическими множествами вида

    и

соответственно. Числа определяются по заданным уровням значимости из таблиц допредельных (или предельных, если очень велико) распределений Колмогорова и Смирнова. Сами эти таблицы могут быть взяты, например, из книги [3].

 

А.Д. Манита, 2001-2011