
9.2 Критерий согласия Пирсона
Наше изложение близко к [7, § 30.1] и [13, § 10.4].
Мы рассматриваем независимую выборку
![]() , обозначая неизвестную
функцию распределения
, обозначая неизвестную
функцию распределения ![]() . Нас интересует вопрос о том, согласуются
ли данные наблюдений
. Нас интересует вопрос о том, согласуются
ли данные наблюдений
![]() с простой гипотезой
с простой гипотезой
Вначале разобъем множество
![]() на конечное число непересекающихся подмножеств
на конечное число непересекающихся подмножеств
![]() . Пусть
. Пусть
![]() -- вероятность, соответствующая
функции распределения
-- вероятность, соответствующая
функции распределения ![]() , обозначим
, обозначим
![]() Очевидно, что
Очевидно, что

Теперь сделаем группировку данных аналогично процедуре, описанной в
![]() 6.3,
а именно, определим
6.3,
а именно, определим
Очевидно, что в силу случайных колебаний эмпирические частоты
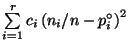 ,
где положительные числа
,
где положительные числа Подчеркнем, что величина
Поведение
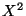 , когда гипотеза
, когда гипотеза
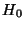 верна.
верна.
Речь идет о поведении при увеличении объема выборки:
![]() .
.
Теорема К. Пирсона. Предположим, что гипотеза
Практический смысл этой теоремы в том, что при большом объеме
выборки распределение ![]() можно считать распределением хи-квадрат
с
можно считать распределением хи-квадрат
с ![]() степенью свободы.
степенью свободы.
Поведение
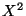 , когда гипотеза
, когда гипотеза
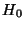 неверна.
неверна.
Предположим теперь, что
![]() и разбиение
и разбиение
![]() таково, что
таково, что
Критерий проверки.
То обстоятельство, что поведение ![]() существенно различно в зависимости
от того верна или нет гипотеза
существенно различно в зависимости
от того верна или нет гипотеза ![]() , дает возможность построить критерий
для ее проверки. Зададимся некоторым уровнем значимости
, дает возможность построить критерий
для ее проверки. Зададимся некоторым уровнем значимости
![]() (допустимой вероятностью ошибки) и возьмем квантиль
(допустимой вероятностью ошибки) и возьмем квантиль
![]() ,
определенную формулой (45):
,
определенную формулой (45):
- если
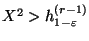 , то гипотеза
, то гипотеза 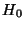 отвергается
(при этом говорят, что выборка обнаруживает значимое отклонение от гипотезы
отвергается
(при этом говорят, что выборка обнаруживает значимое отклонение от гипотезы 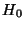 ),
),
- если
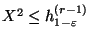 , то гипотеза
, то гипотеза 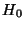 принимается
(говорят, что выборка совместима с гипотезой
принимается
(говорят, что выборка совместима с гипотезой 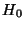 ).
).
При таком решающем правиле мы может допустить ошибку, отвергнув верную гипотезу ![]() .
Из теоремы Пирсона вытекает, что при больших
.
Из теоремы Пирсона вытекает, что при больших ![]() величина вероятности этой
ошибки близка к
величина вероятности этой
ошибки близка к
![]() .
.
Границы применимости критерия на практике.
Утверждения теоремы Пирсона и (52) относятся к пределам при
![]() .
На практике, конечно, мы имеем дело лишь с выборками ограниченного объема.
Поэтому, применяя вышеописанный критерий, необходимо проявлять осторожность.
Согласно рекомендациям, изложенным в [7], применение критерия
дает хорошие результаты, когда все ожидаемые частоты
.
На практике, конечно, мы имеем дело лишь с выборками ограниченного объема.
Поэтому, применяя вышеописанный критерий, необходимо проявлять осторожность.
Согласно рекомендациям, изложенным в [7], применение критерия
дает хорошие результаты, когда все ожидаемые частоты
![]() .
Если же какие-то из этих чисел малы, рекомендуется, укрупняя некоторые группы,
перегруппировать данные таким образом, чтобы ожидаемые частоты всех групп были
не меньше десяти. Если число
.
Если же какие-то из этих чисел малы, рекомендуется, укрупняя некоторые группы,
перегруппировать данные таким образом, чтобы ожидаемые частоты всех групп были
не меньше десяти. Если число ![]() достаточно велико, то, как указывается
в книге [13], порог для ожидаемых частот может быть понижен до
достаточно велико, то, как указывается
в книге [13], порог для ожидаемых частот может быть понижен до ![]() или даже до
или даже до ![]() , если
, если ![]() имеет порядок нескольких десятков.
имеет порядок нескольких десятков.
|
След.: 9.3 Критерий согласия для ...
Пред.: 9.1 Простые и сложные ... Вверх: 9 Статистические гипотезы ... |
Оглавление
Предметный указатель |
