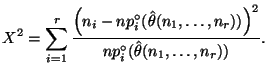9.3 Критерий согласия для сложных гипотез
На практике задача о согласии данных наблюдений с некоторым
совершенно конкретным распределением, рассмотренная в
![]() 9.2,
встречается реже, чем задача проверки сложной гипотезы, которую мы рассматриваем
ниже. Итак, рассмотрим независимую выборку
9.2,
встречается реже, чем задача проверки сложной гипотезы, которую мы рассматриваем
ниже. Итак, рассмотрим независимую выборку
![]() , соответствующую
неизвестной функции распределения
, соответствующую
неизвестной функции распределения ![]() . Поставим вопрос о том, согласуются
ли данные наблюдений
. Поставим вопрос о том, согласуются
ли данные наблюдений
![]() со сложной гипотезой
со сложной гипотезой
Группируя данные аналогично
![]() 9.2 и вычисляя
9.2 и вычисляя
![]() по функции распределения
по функции распределения
![]() , обнаруживаем, что теперь эти
вероятности являются функциями от неизвестного параметра:
, обнаруживаем, что теперь эти
вероятности являются функциями от неизвестного параметра:
Пусть числа ![]() ,
,
![]() , вычислены по выборке согласно
формуле (50). Запишем следующую функцию правдоподобия
, вычислены по выборке согласно
формуле (50). Запишем следующую функцию правдоподобия
Справедлив следующий вариант теоремы Пирсона5: Предположим, что гипотеза
Заметим, что по сравнению с теоремой из
![]() 9.2 за замену
9.2 за замену
![]() -мерного неизвестного параметра его оценкой нам пришлось ``заплатить''
-мерного неизвестного параметра его оценкой нам пришлось ``заплатить''
![]() степенями свободы в предельном распределении хи-квадрат.
степенями свободы в предельном распределении хи-квадрат.
В дальнейшем, фиксируя
![]() и выбирая критическое множество
и выбирая критическое множество
Все примечания относительности применимости этого критерия, сделанные в
![]() 9.2,
разумеется, остаются в силе.
9.2,
разумеется, остаются в силе.
То обстоятельство, что оценка
![]() ,
которую мы используем в определении (53), зависит от выборки
только через значения
,
которую мы используем в определении (53), зависит от выборки
только через значения
![]() , является важным для утверждения сформулированной
выше теоремы. Как показано в книге [13, § 10.6], замена параметра
, является важным для утверждения сформулированной
выше теоремы. Как показано в книге [13, § 10.6], замена параметра
![]() произвольной его оценкой по выборке
произвольной его оценкой по выборке
![]() приводит
к тому, что
приводит
к тому, что
![]() больше не является удовлетворительной аппроксимацией
для
больше не является удовлетворительной аппроксимацией
для ![]() .
.