ЛАБОРАТОРИЯ МАТЕМАТИЧЕСКИХ ПРОБЛЕМ ЕСТЕСТВЕННЫХ НАУК КАФЕДРЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ МЕХАНИКО-МАТЕМАТИЧЕСКОГО ФАКУЛЬТЕТА МГУ

Публикации | Сотрудники лаборатории | Контакты | Кафедра дифференциальных уравнений

Лаборатория математических проблем естественных наук – это лаборатория промышленной («интердисциплинарной») математики на механико-математическом факультете МГУ.
В течение последних лет группа сотрудников кафедры дифференциальных уравнений МГУ и Института проблем механики РАН активно участвовала в ряде прикладных научных проектов с российскими корпорациями «Уралхим» и «Уралкалий», с Университетом штата Пенсильвания (США), НТЦ «Космонит» ОАО «Российские космические системы», а также с некоторыми другими промышленными организациями. Результаты этого сотрудничества стали основой для создания прикладной лаборатории.

Математическая биология

1. Хемотаксис

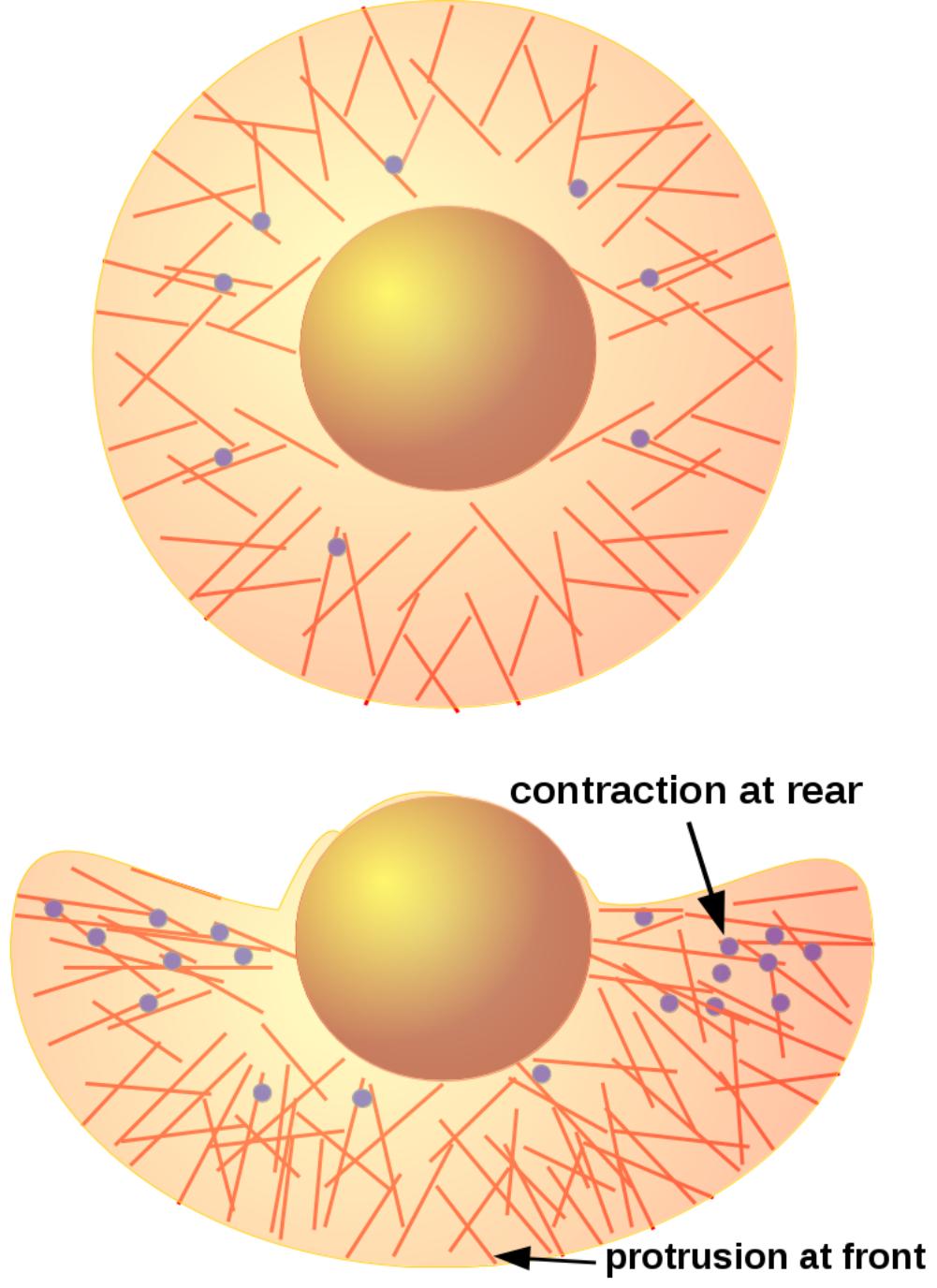
Направленное движение клеток и ансамблей клеток в живых организмах давно привлекало внимание биологов, биохимиков, биофизиков и математиков, создающих математические модели такого движения. Примером может служить направленное движение кровяных частиц к месту пореза на теле человека, выталкивание клетками инородных частиц, преследование «врагов»-бактерий, согласованное движение клеток эпителия к месту ранения с целью регенерации поврежденных тканей и пр. Каким-то образом клетка или группа клеток решает, куда и когда надо «идти».
Проблема направленного движения отдельных клеток и ансамбля клеток как целого – одна из самых актуальных и современных задач современной математической биологии. Построение адекватных математических моделей такого движения очень актуально для проблем медицины и фармакологии. Кроме того, это направление приводит к новым и интересным задачам теории уравнений с частными производными: существование решений типа «бегущих волн» у уравнений и систем параболического типа с нелинейными членами; корректность постановки краевых задач для нелинейных параболических и парабо-эллиптических систем с неклассическими краевыми условиями – они могут быть заданы на неизвестной границе, которая движется с течением времени, и нелокальными, т.е. связывать граничные значения в различных точках границы.
Математические постановки таких задач еще далеко не изучены как с точки зрения качественных свойств, так и с точки зрения построения адекватных численных алгоритмов решения и построения алгоритмов идентификации параметров. Мы собираемся продолжить исследования с точки зрения математики.

2. Физика активных гелей

Очень интересными с теоретической и практической точки зрения являются задачи построения адекватных моделей сред с «активными» элементами. Например, в работах Л. Берлянда показано строгими методами на основе математической модели, что в жидкости с бактериями, которые могут активно реагировать на окружающую обстановку, резко меняется (уменьшается в разы!) вязкость. Позднее эти работы послужили основой для создания уже чисто химическими методами (при отсутствии каких-либо «живых» элементов) жидкостей с очень низкой вязкостью, которые используются в качестве чернил для современных 3D-принтеров. Мы считаем эти исследования очень перспективными. Наша группа предлагает продолжить их, расширив круг моделей сред с активными элементами. Это могут быть иные сплошные среды (не обязательно классические жидкости) и в качестве активных элементов рассмотрены не обязательно бактерии.

Искусственный интеллект

Часто модели исследуемых систем могут содержать параметры, которые не удается получить из «первых принципов», они имеют «феноменологическую» природу, но они могут быть определены путем настройки параметров модели под результаты тех или иных экспериментов. Здесь существенную помощь может оказать применение современных методов искусственного интеллекта, применение электронных самообучающихся систем. Большую роль будут играть различные методы оптимизации, с помощью которых может быть осуществлен поиск неизвестных параметров модели. Здесь к минимуму должна быть сведена невязка между некоторым набором экспериментальных данных и набором расчетных данных, в которые входят параметры, величину которых нужно идентифицировать.

Суперкомпьютер «Ломоносов», установленный в Московском университете в 2009 году

Обратные задачи электродинамики

1. Голографические методы

Исследование субволновых возможностей голографических методов. Проблемы восстановления голографическими методами пространственной структуры молекулы по интерференционной картине рассеянного на молекуле расходящегося электронного пучка и опорного также расходящегося электронного пучка. Возможные применения– синтез новых лекарственных препаратов. Ниже приведен результат компьютерного моделирования процесса восстановления голографическими методами пространственной структуры молекулы спирта (С₂H₅OH).

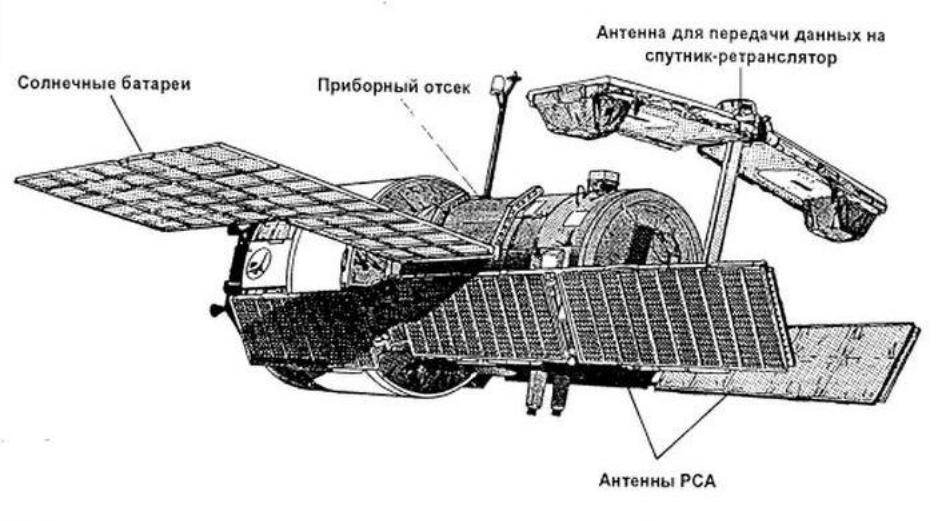
2. Радиометрические исследования мирового океана

Проблемы радиометрических исследований мирового океана, совместно с ОАО «Космонит» ОАО «Российские космические системы». Основная проблема – восстановление параметров морского волнения по собственному радиоизлучению океана. Написана и отлажена программа моделирования собственного радиоизлучения участка морской поверхности.

Активная космическая радиолокация:

Алмаз-1A

Радиометры

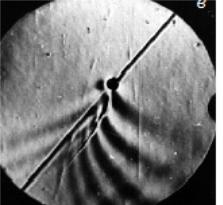
Внутренние волны в океане. Теория и эксперимент

Ниже приведены результаты математического моделирования внутренних волн, возбужденных движущимся источником, а также результаты эксперимента в лаборатории гидромеханики Института проблем механики РАН.

Результат математического моделирования

Результат эксперимента

Математическое моделирование рудников

Совместные проекты с компаниями «Уралхим» и «Уралкалий» относятся к математическому моделированию упругопластических свойств соляных пород, процессов ползучести, пластичности и трещинообразования в соляных рудниках Пермского края. Совместная деятельность тесно связана с вопросами безопасности горных разработок в калийных шахтах. Эта тематика в последнее время стала очень актуальной в связи с несколькими авариями на соляных шахтах в окрестностях города Березняки. Планируется разработка математической модели всей калийной выработки в г. Березняки (Пермский край) с целью прогнозирования явлений, которые могут привести к авариям в будущем.
Условное название проекта – «виртуальный рудник», в настоящее время получены аналитические представления для эффективных характеристик процессов ползучести соляных пластов с глинистым прослойками.

Слоистые соляные горные породы (г. Березняки)

Финансовая математика

В течение почти двадцати последних лет на кафедре дифференциальных уравнений работает семинар «Математические модели в экономике» (рук. - проф. О.С. Розанова и А.С. Шамаев). Среди участников семинара около 150 дипломников механико-математического факультета, дипломные работы которых были так или иначе связаны с математическими моделями в экономике. Нас интересуют более всего оригинальные и новые постановки краевых задач для дифференциальных и интегро-дифференциальных уравнений и систем, которые возникают (а это именно так!) в современной финансовой математике и экономике вообще. В качестве примеров приводим три кандидатские диссертации участников нашего семинара - К. Хорева (краевые задачи с неизвестной границей, связанные с анализом кредитных рынков), Г. Камбарбаевой (уравнения типа Фоккера-Планка, возникающие в проблеме управления инвестиционным портфелем, активы которого моделируются стохастическими дифференциальными уравнениями), А. Чечкина (задачи Коши для параболических уравнений с полиномиальными коэффициентами, возникающие в проблемах управления активами и проблемах хеджирования), статью А. Асекова и А. Шамаева, посвященную построению аналога эффективного фронта в задаче управления активами, в которой используются теоремы Фредгольма для эллиптических операторов в неограниченных областях. Интересные и новые математические проблемы возникают при построении моделей активов с учетом психологии участников рынка (О.С. Розанова).
Мы собираемся продолжать практически значимые исследования по финансовой математике в рамках создаваемой лаборатории.

Динамика атмосферы

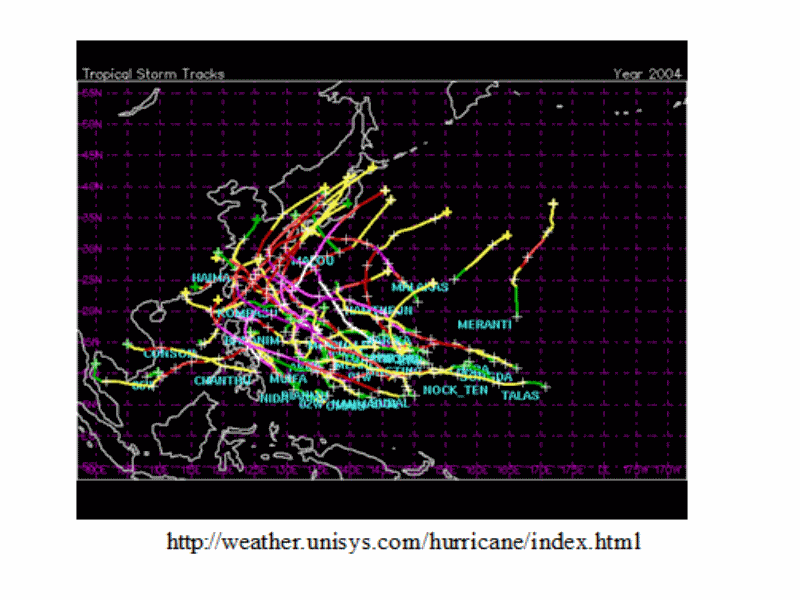
Исследование больших атмосферных вихрей

Изучение возможных траекторий долгоживущих крупномасшнабных атмосферных вихрей (тайфунов или ураганов), сравнение с реальными траекториями. Исследование их структуры, условий образования, устойчивости в рамках двумерных и трехмерных моделей. Аппроксимации полной модели. Изучение влияния топографии на траекторию движения вихрей. Сотрудничество с учеными Тайваня, Китая, США, Франции.