
7.2 Система нормальных уравнений
Существует следующая модификация линейной модели. Пусть
![]() -- вектор-столбец неизвестных параметров. Предположим, что мы не можем непосредственно
наблюдать
-- вектор-столбец неизвестных параметров. Предположим, что мы не можем непосредственно
наблюдать
![]() , но можем измерить их некоторые
линейные комбинации прибором, допускающим независимые случайные ошибки. Сформулируем
точную модель. Пусть
, но можем измерить их некоторые
линейные комбинации прибором, допускающим независимые случайные ошибки. Сформулируем
точную модель. Пусть
![]() --
-- ![]() -матрица,
-матрица,
![]() -- вектор-столбец результатов измерений,
-- вектор-столбец результатов измерений,
![]() -- вектор-столбец ошибок,
-- вектор-столбец ошибок,
![]() --
--
![]() .
Основное предположение состоит в том, что
.
Основное предположение состоит в том, что ![]() и
и
Рассмотрим подпространство в
![]() , порожденное столбцами матрицы
, порожденное столбцами матрицы ![]() :
:
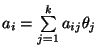 ,
то задача сведется к виду (37). Согласно
,
то задача сведется к виду (37). Согласно

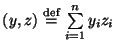 .
Пользуясь свойствами скалярного произведения, получим
.
Пользуясь свойствами скалярного произведения, получим
Таким образом,
![]() может быть найдено из системы линейных уравнений (39),
именуемой системой нормальных уравнений.
Если матрица
может быть найдено из системы линейных уравнений (39),
именуемой системой нормальных уравнений.
Если матрица ![]() имеет полный ранг, то квадратная матрица
имеет полный ранг, то квадратная матрица
![]() обратима и
обратима и