8.1 Понятие доверительного интервала
Будем считать, что независимая выборка
![]() взята из распределения,
зависящего от скалярного параметра
взята из распределения,
зависящего от скалярного параметра
![]() . Будем обозначать
через
. Будем обозначать
через
![]() распределение вероятностей, соответствующее значению
распределение вероятностей, соответствующее значению
![]() неизвестного параметра.
неизвестного параметра.
![]() -доверительным интервалом
называется интервал вида
-доверительным интервалом
называется интервал вида
![]() где
где ![]() такой, что
такой, что
Другими словами, доверительный интервал обладает тем свойством, что, во-первых,
его границы вычисляются исключительно по выборке (и, следовательно, не зависят
от неизвестного параметра), и, во-вторых, он накрывает неизвестный параметр
с вероятностью ![]() .
.
Значение доверительной вероятности
![]() выбирается заранее, этот
выбор определяется конкретными практическими приложениями.
выбирается заранее, этот
выбор определяется конкретными практическими приложениями.
Смысл величины
![]() -- вероятность допустимой ошибки. Часто берут значения
-- вероятность допустимой ошибки. Часто берут значения
![]() и т.п.
и т.п.
Ниже мы приводим один из методов построения доверительных интервалов. Он состоит из трех этапов.
- Выбираем функцию
 , зависящую от выборки и от неизвестного
параметра, такую, что ее функция распределения
не зависит от неизвестного параметра
, зависящую от выборки и от неизвестного
параметра, такую, что ее функция распределения
не зависит от неизвестного параметра
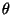 .
.
- Выбираем два числа
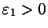 и
и
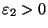 таким
образом, чтобы
таким
образом, чтобы
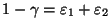 . Подбираем
. Подбираем
 и
и
 , удовлетворяющие условиям
, удовлетворяющие условиям
Таким образом,
причем и
и
 не зависят от
не зависят от 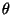 .
.
- Решим двойное неравенство
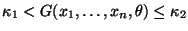 относительно
относительно 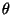 . В том случае, когда его решением является интервал,
обозначим его левый и правый концы через
. В том случае, когда его решением является интервал,
обозначим его левый и правый концы через
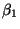 и
и
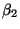 соответственно. Естественно, они зависят от выборки:
соответственно. Естественно, они зависят от выборки:
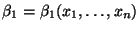 ,
,
 . В силу (42)
Следовательно,
. В силу (42)
Следовательно,
 --
искомый
--
искомый  -доверительный интервал.
-доверительный интервал.
Описанная процедура, разумеется, не является универсальной. Во-первых, вопрос
о выборе функции ![]() решается в каждом конкретном случае и по этому поводу
нет общих рекомендаций. Во-вторых, совершенно не гарантировано, что решением
неравенства в п. 3 будет интервал конечной длины. Вместе с тем, во многих важных
случаях изложенный выше метод приводит к хорошим доверительным интервалам. Например,
оправдано применение такого метода в случае, когда при каждой фиксированной
выборке
решается в каждом конкретном случае и по этому поводу
нет общих рекомендаций. Во-вторых, совершенно не гарантировано, что решением
неравенства в п. 3 будет интервал конечной длины. Вместе с тем, во многих важных
случаях изложенный выше метод приводит к хорошим доверительным интервалам. Например,
оправдано применение такого метода в случае, когда при каждой фиксированной
выборке
![]() функция
функция
![]() является
строго монотонной и непрерывной по переменной
является
строго монотонной и непрерывной по переменной ![]() .
.
В силу неоднозначности выбора функции ![]() и чисел
и чисел
![]() и
и
![]() , можно заключить, что
, можно заключить, что ![]() -доверительный
интервал неединственен.
-доверительный
интервал неединственен.
Пусть
![]() -- независимая выборка из равномерного распределения
в отрезке
-- независимая выборка из равномерного распределения
в отрезке
![]() с неизвестным параметром
с неизвестным параметром ![]() :
:
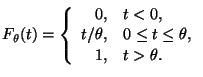
- Рассмотрим функцию
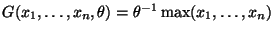 .
Вычислим ее функцию распределения:
.
Вычислим ее функцию распределения:

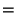
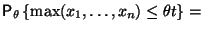
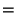
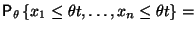
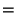
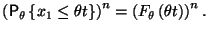
Таким образом,и, следовательно, не зависит от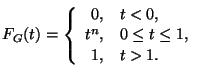
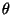 .
.
- Зафиксируем
 так, чтобы
так, чтобы
 .
Тогда
.
Тогда
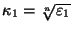 и
и
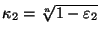 удовлетворяют (41).
удовлетворяют (41).
- Решая неравенство
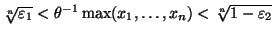 ,
получаем
,
получаем  -доверительный интервал для
-доверительный интервал для 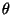 :
:
Очевидно, что следует отдавать предпочтение тем ![]() -доверительным
интервалам, у которых длина короче.
-доверительным
интервалам, у которых длина короче.
Показать, что при
![]() математическое ожидание длины
доверительного интервала (43) стремится к нулю.
математическое ожидание длины
доверительного интервала (43) стремится к нулю.
|
След.: 8.2 Вероятностные распределения, связанные ...
Пред.: 8 Доверительные интервалы ... Вверх: 8 Доверительные интервалы ... |
Оглавление
Предметный указатель |