
3.1 Общее определение вероятностного пространства
В отличие от рассматривавшейся нами ранее дискретной ситуации,
где вероятностным пространством была названа пара
![]() , под
общим вероятностным пространством согласно аксиоматике Колмогорова
следует понимать тройку объектов
, под
общим вероятностным пространством согласно аксиоматике Колмогорова
следует понимать тройку объектов
![]() , смысл которых раскрывается
следующими определениями.
, смысл которых раскрывается
следующими определениями.
Определение 3.1
Вероятностным пространством
называется тройка
 , где
, где
|
|
|
|
Определение 3.2
Система
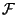 подмножеств множества
подмножеств множества 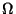 называется
называется
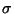 -алгеброй, если
-алгеброй, если
- 1)
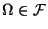 (
(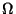 -- единица в
-- единица в 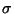 -алгебре)
-алгебре)
- 1а)

- 2) Если
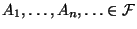 , то
, то
 (другими словами,
(другими словами,
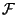 замкнуто относительно счетных объединений)
замкнуто относительно счетных объединений)
- 2а) Если
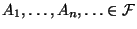 , то
, то
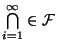 (другими словами,
(другими словами,
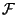 замкнуто относительно счетных пересечений)
замкнуто относительно счетных пересечений)
- 3) Если
 , то
, то
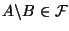 .
.
Замечание 3.1
Достаточно требовать лишь выполнения свойств 1), 2) и 3),
т.к. свойства 1a) и 2a) следуют из них.
Определение 3.3
Вероятностной мерой
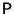 называется отображение
называется отображение
 , обладающее следующими
свойствами:
, обладающее следующими
свойствами:
-
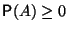 ,
,
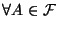 ,
,
-
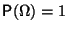 ,
,
- Если
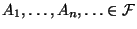 и
и
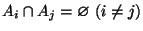 ,
то
,
то
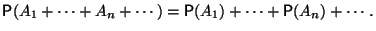
В рамках такого подхода элементы
![]() и только они трактуются
как события.
и только они трактуются
как события.
Замечание 3.2
Дискретное вероятностное пространство вкладывается
в эту схему. В качестве 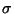 -алгебры событий
-алгебры событий
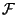 здесь
выступает множество всевозможных подмножеств дискретного множества
здесь
выступает множество всевозможных подмножеств дискретного множества 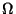 .
.
Замечание 3.3
Для более, чем счетных 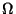 , как правило, нельзя
выбрать в качестве
, как правило, нельзя
выбрать в качестве 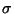 -алгебры
-алгебры
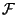 множество всех
подмножеств
множество всех
подмножеств 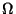 и корректно задать на ней вероятностную меру. Это означает,
что не каждое подмножество
и корректно задать на ней вероятностную меру. Это означает,
что не каждое подмножество 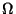 есть событие.
есть событие.