
2.4 Общие свойства математического ожидания
Предложение 2.1
Имеют место следующие свойства.
- Если случайная величина
 постоянна, то есть, для некоторой константы
постоянна, то есть, для некоторой константы
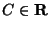 имеет место
имеет место
 , то
, то
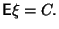
-
 для любого
для любого
 .
.
- Если
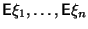 существуют, то
существуют, то
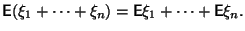
- Если
 и
и
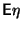 существуют и
существуют и
 для всех
для всех
 , то
В частности, если
, то
В частности, если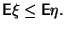

 , то математическое
ожидание
, то математическое
ожидание
 неотрицательно при условии, что оно существует.
неотрицательно при условии, что оно существует.
Доказательство.
Свойства 1) и 2) очевидны. Докажем 3).
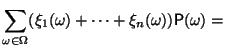 |
|||
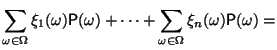 |
|||
Докажем 4). Так как при каждом

![]()
Замечание 2.2
Свойства 2) и 3) называются свойствами линейности математического ожидания. Обратим внимание на то, что линейность имеет место всегда, без каких-либо дополнительных предположений (кроме предположения о существовании самих математических ожиданий).