Средняя сложность "почти всех" булевых функций
Рассматрим задачу об определении средней сложности "почти всех" булевых функций n переменных.
Покажем, что средняя сложность почти каждой булевой функции с точностью до постоянного
множителя совпадает с ее обычной сложностью.
Теорема. Пусть n неограниченно возрастает. Тогда:
(i) для почти каждой булевой функции f, зависящей от n переменных
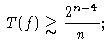
(ii) для каждой булевой функции f, зависящей от n переменных
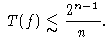
Доказательство. Пусть f - булева функция n переменных, P - программа, вычисляющая f. Каждому двоичному набору x длины n, рассматриваемому как двоичная запись натурального числа, поставим в соответствие его номер
NP(x) - целое число большее нуля, не превосходящее 2n и такое, что
NP(x) < NP(y), если TP(x) < TP(y); NP(x) < NP(y), если TP(x) = TP(y) и x < y.
Оценим число булевых функций средняя сложность каждой из которых не превосходит величины 2n-4/n. Пусть f - одна из таких функций, P - минимальная программа, вычисляющая f. Рассмотрим набор x0 такой, что NP(x0) = 2n-1. Тогда из определения средней сложности следует, что
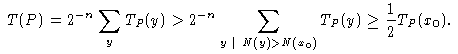
Поэтому, TP(x0)<2T(f).
Так как T(f) не больше чем 2n-4/n, то легко видеть, что
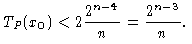
| (1) |
Каждая функция однозначно определяется первыми TP(x0) операторами своей минимальной программы P и двоичным вектором длины не более чем 2n-1, состоящим из значений функции f на тех аргументах, время работы P на которых больше времени работы этой программы на x0. Обозначим через N0 число различных программ, состоящих не более чем из TP(x0) операторов. Тогда число функций, средняя сложность которых не превосходит 2n-4/n, ограничена сверху величиной
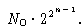
Оценим N0.
Любая программа P определяется списком своих операторов pi, каждый из которых однозначно задается следующими данными:
типом оператора - возможны всего два варианта, оператор может быть либо функциональным, либо оператором остановки;
двуместной булевой функцией fi, вычисляемой функциональным оператором (для оператора остановки эта информация опускается) - существует всего 16 различных двуместных булевых функций;
номером переменной, выходной или внутренней, являющейся выходом функционального оператора (для оператора остановки эта информация опускается) - если программа P состоит из L операторов, то общее число внутренних и выходной переменных не превосходит L и без ограничения общности полагаем, что внутренние переменные нумеруются числами от 1 до L -1, а выходной переменной присваивается номер L, номерами переменных, независимых или внутренних, являющихся входами оператора - полагаем, что независимые переменные нумеруются числами от L+1 до L+n, поэтому общее число пар номеров не превосходит (L+n)2.
Поэтому для числа N, равного числу различных программ, состоящих из L операторов, справедливо неравенство
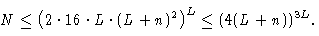
Подставляя в это неравенство вместо L величину TP(x0) и учитывая полученное выше для этой величины неравенство
(1), видим, что при n > 4 имеет место неравенство

Следовательно, число функций, средняя сложность которых не превосходит 2n-4/n, не больше чем
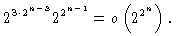
Таким образом, средняя сложность почти каждой булевой
функции, зависящей от n переменных, не меньше чем 2n-4/n. Первое неравенство теоремы доказано.
(ii) Каждому двоичному набору 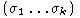 поставим в соответствие его номер
поставим в соответствие его номер
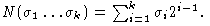
Положим параметр s равным целой части снизу разности n - log2 n. Функцию f разложим по первым n-s переменным:
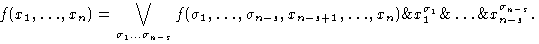
Программу, вычисляющую функцию f, представим в следующем виде
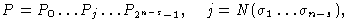 где Pj - программа, вычисляющая функцию
где Pj - программа, вычисляющая функцию
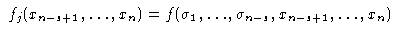
и прекращающая работу программы
P, если
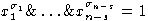 .
.
Так как сложность произвольной функции, зависящей от s переменных, асимптотически не превосходит
2s/s, то и L(Pj) асиптотически не больше 2s/s. Поэтому
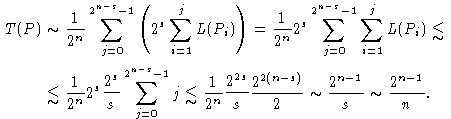 Теорема доказана.
Теорема доказана.
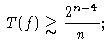
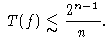
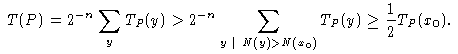
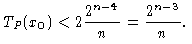
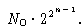
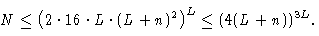

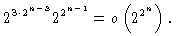
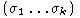 поставим в соответствие его номер
поставим в соответствие его номер
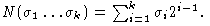
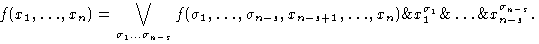
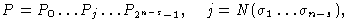
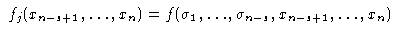
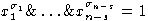 .
.