---

Straight-line Programs with conditional stop

---

Let P₂(2) be the set of Boolean functions depending on two variables. Let X={x₁,...,x_n} be a set of independent variables, Y={y₁,...,y_l} be a set of inner variables, and Z={z₁,...,z_m} be a set of output variables. Assume that A is in YÈ Z and B, C belong to Y È Y È Z. Let f be a function from P₂(2). An expression

p:    A = f(B, C)

is called a functional instruction. Here, A is called the output of the functional instruction p, and B, C are called inputs of this instruction. Let A be an element of Y È Y È Z. An expression  

p:    Stop(A)

is called a stop instruction. Here, A is called the input of stop instruction p.
A straight-line program is a sequence P = p₁... p_i...p_L whose elements are instructions and each input of instruction p_j, j {1,2,..., s}, is either an independent variable or the output of some functional instruction p_i, i<j.
A straight-line program works at discrete moments of time t = 0,1,2,... and does not change the values of independent variables. Let us define the values of inner variables y_i(x; t) and output variables z_j(x; t) of P at any time on x = (x₁,...,x_n) by induction:

At the initial time, t = 0, the values of all inner and output variables are undefined;

If an inner variable y_i (output variable z_j) is not the output of an instruction p_t, then we set

y_i(x; t) = y_i(x; t-1),       z_j(x; t) = z_j(x; t-1);

If an inner variable y_i (output variable z_j) is the output of p_t and the input values of p_t equal B(x; t-1) and C(x; t-1) at the moment t-1, then we set

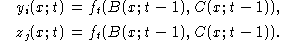
The value of p_t on the tuple x = (x₁,...,x_n) is the value of its output at t, which is denoted by p_t(x).
In each program P all stop instructions are assumed to be ordered. Denote by s_j the jth stop instruction.
An instruction p_i (variable x_l) is called a zero argument of stop instruction s_j = p_j' iff the output of p_i (variable x_l) is the input of s_j. The zero argument of s_j is denoted by q_j.
We say that kth stop instruction s_k terminates the execution of P on the tuple x iff

q₁(x) =... = q_k-1(x) = 0,    q_k(x) = 1.

The result of the execution of P on x is denoted by P(x) and its jth component P_j(x) is defined in the following way:

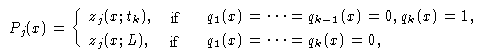
e.g., P_j(x) equals the value of the jth output variable at the stop moment. It is easy to see that

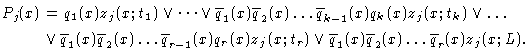
Let L(P) denote the number of instructions in P. L(P) is called the complexity of P. The execution time T_P(x) of P on tuple x is the number of instructions executed before the endpoint of P, i.e., T_P(x)=k iff the kth instruction of P = p₁... p_i...p_L is the stop instruction s_t and for zero argument q_t(x) we have q_t(x) = 1 on x and q_j(x) = 0 for all j<t. If q_j(x) = 0 for all j, then all the instructions in P are executed and in this case T_P(x) = L(P). The quantity

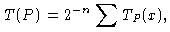
(where summation is performed over all binary tuples of length n) is called the average execution time of P. If for a Boolean function (operator) f and any tuple x we have f(x) = P(x), then the program P is said to compute f. The quantity

T(f) = min T(P)

(where the minimum is taken over all programs computing f) is called the average execution time (average complexity) of f. A program P that computes f and is such that T(P) = T(f) is called a minimal program. The number of elements of a minimal Boolean circuit that realizes f over the basis of all two-place functions is called the complexity of f and is denoted by L(f).

It is easy to see that Boolean circuits are a special case of straight-line programs with a conditional stop. Any circuit can be treated as a program with no stop instruction. Thus T(P) = L(f).

---