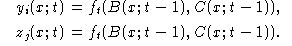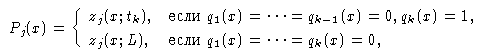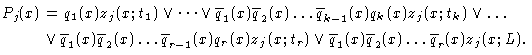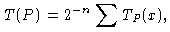Неветвящиеся программы
Пусть P2(2) - множество всех не более чем двухместных булевых функций, X={x1,...,xn} - множество независимых булевых переменных, Y={y1,...,yl} - множество внутренних переменных, Z={z1,...,zm} - множество выходных переменных. Пусть A принадлежит объединению множеств Y и Z, B и C принадлежат объединению множеств X, Y и Z, f является функцией из множества P2(2). Выражение
p: A = f(B, C)
назовем функциональным оператором. Величину A назовем выходом функционального оператора p, а величины B, C назовем входами этого оператора. Пусть, далее, A - элемент объединения
множеств X, Y и Z. Выражение
p: Stop(A)
назовем оператором остановки. Величину A назовем входом оператора остановки p.
Пусть P = p1... pi...pL - последовательность операторов. Последовательность P назовем неветвящейся программой с условной остановкой, если каждый вход оператора pj, где j принадлежит {1,2,..., s}, есть либо независимая переменная, либо выход некоторого функционального оператора pi при i<j.
Неветвящаяся программа работает в дискретные моменты времени t = 0,1,2,... и не изменяет значения независимых переменных. Значения внутренних yi(x; t) и выходных zj(x; t) переменных программы P в произвольный момент времени t на наборе независимых переменных x = (x1,...,xn) определим индуктивно:
В начальный момент времени, t = 0, значения всех внутренних и выходных переменных считаем неопределенными;
Если внутренняя переменная yi (выходная переменная zj) не является выходом оператора pt, то положим
yi(x; t) = yi(x; t-1),
zj(x; t) = zj(x; t-1);
Если внутренняя переменная yi (выходная переменная zj) является выходом оператора pt и значения входов оператора pt в момент времени t-1 равны B(x; t-1) и C(x; t-1), то положим
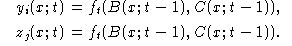
Значением оператора pt на наборе независимых переменных x = (x1,...,xn) назовем значение его выхода в момент времени t и обозначим через pt(x).
В каждой программе P перенумеруем в естественном порядке все операторы остановки. Через sj будем обозначать j-й оператор остановки программы.
Оператор pi (переменную xl) назовем нулевым аргументом оператора остановки sj = pj' если
выход оператора pi (переменная xl) является входом оператора sj. Нулевой аргумент оператора sj обозначим через qj.
Будем говорить, что k-й оператор остановки sk останавливает вычисления программы P на наборе x, если
q1(x) =... = qk-1(x) = 0, qk(x) = 1.
Результат действия программы P на наборе x обозначим через P(x) и его j-ю компоненту Pj(x) определим следующим образом:
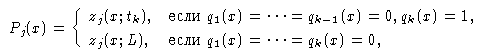
т.е. Pj(x) равно значению j-й выходной переменной в момент остановки программы. Легко видеть, что
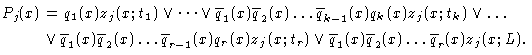
Сложностью L(P) программы P назовем число операторов этой программы.
Временем работы TP(x) программы P на наборе переменных x назовем число операторов, выполненных до остановки программы, т. е.
TP(x)=k, если на k-м месте в программе P
стоит оператор остановки st,
значение qt(x) = 1
его нулевого аргумента
на наборе переменных x равно единице, и qj(x) = 0 при
всех j меньших t.
Если в программе P все qj(x) = 0,
то выполняются все операторы программы и в этом случае
TP(x) = L(P). Величину
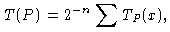
где суммирование производится по всем двоичным наборам длины n, назовем средним временем работы программы P. Если для некоторого булевого оператора f и любого двоичного набора x справедливо равенство f(x) = P(x), то будем говорить, что программа P вычисляет оператор f. Величину
T(f) = min T(P),
где минимум берется по всем программам, вычисляющим f, назовем средним временем вычисления (средней сложностью) оператора f. Программу P, вычисляющую оператор f, для которой справедливо равенство T(P) = T(f), назовем минимальной программой. Число элементов минимальной схемы из функциональных элементов, реализующей функцию f в базисе из всех не более чем двухместных булевых функций назовем сложностью f и обозначим символом L(f).
Отметим, что неветвящаяся программа, не содержащая операторы остановки и вычисляющую функцию отличную от независимой переменной, является обычной схемой из функциональных элементов.