УДК 517.51
О равенстве Парсеваля для произведения функций / Лукашенко Т.П. // Вестн. Моск. ун-та. Сер. 1,
Математика. Механика.
![]() C. 32-40.
C. 32-40.
Получены результаты о равенстве Парсеваля в случае,
когда наряду с функциями ![]() и
и ![]() интегрируемо по Лебегу
(или в некотором другом смысле) и их произведение
интегрируемо по Лебегу
(или в некотором другом смысле) и их произведение ![]() . Доказаны
следующие теоремы.
. Доказаны
следующие теоремы.
Теорема. Для любых ![]() -периодических
интегрируемых по Лебегу неотрицательных функций
-периодических
интегрируемых по Лебегу неотрицательных функций ![]() и
и ![]() ,
произведение
,
произведение ![]() которых неинтегрируемо по Лебегу, существуют такие
которых неинтегрируемо по Лебегу, существуют такие
![]() -периодические интегрируемые по Лебегу неотрицательные функции
-периодические интегрируемые по Лебегу неотрицательные функции
![]() и
и ![]() ,
,
![]() ,
,
![]() , произведение которых
, произведение которых ![]() равно нулю
всюду, но ряд
равно нулю
всюду, но ряд
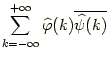 не суммируется методом Абеля,
а значит, всеми методами Чезаро и методом Римана
не суммируется методом Абеля,
а значит, всеми методами Чезаро и методом Римана ![]() .
.
Теорема. Если ![]() и
и ![]() - такие
- такие ![]() -периодические
комплекснозначные интегрируемые в смысле широкого интеграла Данжуа
функции с почти всюду дифференцируемыми первообразными, что
произведение
-периодические
комплекснозначные интегрируемые в смысле широкого интеграла Данжуа
функции с почти всюду дифференцируемыми первообразными, что
произведение ![]() интегрируемо по Лебегу, где
интегрируемо по Лебегу, где
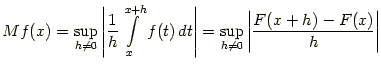 -
неабсолютная максимальная функция Харди-Литлвуда функции
-
неабсолютная максимальная функция Харди-Литлвуда функции
![]() , то выполняется равенство Парсеваля для метода суммирования Римана
, то выполняется равенство Парсеваля для метода суммирования Римана
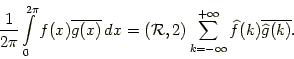
Библиогр. 10.
