УДК 511
Об оценках полных рациональных тригонометрических
сумм и сумм характеров Дирихле / Ходжаев Н.М., Чубариков В.Н. // Вестн. Моск. ун-та. Сер. 1,
Математика. Механика.
![]() C. 17-23.
C. 17-23.
Пусть ![]() -- множество многочленов
-- множество многочленов
![]() с условием
с условием
![]() и
и
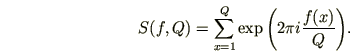
В работе доказаны следующие теоремы.
Теорема 1
Пусть
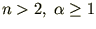 и
и 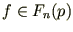 . Тогда имеем
. Тогда имеем
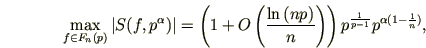
где постоянная в знаке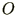 абсолютная. Более точно, справедливо неравенство
абсолютная. Более точно, справедливо неравенство
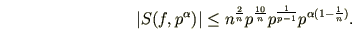
где постоянная в знаке
Теорема 2
Существует положительная постоянная 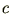 , такая, что
при условии справедливости некоторых гипотез для
, такая, что
при условии справедливости некоторых гипотез для 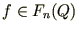 имеет место оценка
имеет место оценка
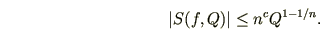
Более того, можно взять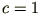 .
.
Более того, можно взять
Теорема 3
Пусть
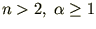 и
и 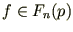 . Тогда имеем
. Тогда имеем
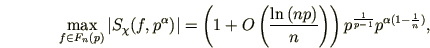
где
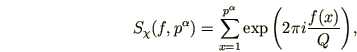
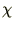 -- примитивный характер Дирихле по модулю
-- примитивный характер Дирихле по модулю 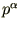 ;
постоянная в знаке
;
постоянная в знаке  абсолютная. Более точно, справедливо неравенство
абсолютная. Более точно, справедливо неравенство
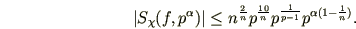
где
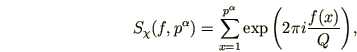
Библиогр. 16.
