УДК 517.518.124+517.518.454
Об интеграле Римана-Стилтьеса и равенстве Парсеваля / Лукашенко Т.П. // Вестн. Моск. ун-та. Сер. 1,
Математика. Механика.
![]() C. 00-00.
C. 00-00.
Доказано, что если 2![]() -периодическая функция
-периодическая функция ![]() и функция
и функция
![]() , являющаяся суммой 2
, являющаяся суммой 2![]() -периодической и линейной функций,
интегрируемы по Лебегу,
-периодической и линейной функций,
интегрируемы по Лебегу, ![]() интегрируема на периоде (любом
отрезке длины
интегрируема на периоде (любом
отрезке длины ![]() ) в смысле Римана-Стилтьеса по
) в смысле Римана-Стилтьеса по
![]() ,
то выполняется равенство Парсеваля
,
то выполняется равенство Парсеваля
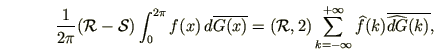
где
Библиогр. 6.
