������� ����������� ������������. ����������, �������� - ����������
��� 519.218.2
���������� �������� � ���������� ��������� ������������.
������ ��������� / ������� �.�. // �����. ����. ��-��. ���. 1,
����������. ��������.
 C. 65-68.
C. 65-68.
��������������� ���������� �������� � ���������� ��������� ������������,
�������� �� ���������
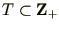 ������������ ��������
������������ ��������
���
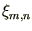
,
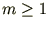
,
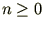
, -- ����������� � ���������
�������������� ��������� �������� �� ���������� �
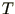
�
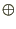
--
��������� ������������� � ������������� �������� ��
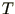
. ��������
������� ������������ ��� ������ ��������, �� ��������� �� ����������
� �����������. ���������� ������ �������� ���������. ��������, ���
� ����������� �� ����, ���������
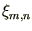
������� �������� ��� ���,
������� ���� ����������� ������������, ���� ������ �� �������������
����� ��������. ����������� ������� ������� ������������ ���������.
����. 1. ��������. 4
![]() C. 65-68.
C. 65-68.
![]() ������������ ��������
������������ ��������

