Вестник Московского Университета. Математика, Механика - Содержание


УДК 511

Об оценке интеграла Виноградова при малом числе переменных / О.В. Тырина // Вестн. Моск. ун-та. Сер. 1, Математика. Механика. 2002. N.1 C. 26-29.

Пусть $n,k,P$ -- натуральные числа, $J=J_{k,n}(P)$ -- число целочисленных решений системы уравнений

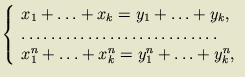
$\displaystyle \left\{\begin{array}{l} x_{1}+\ldots +x_{k}= y_{1}+\ldots +y_... ..._{1}^{n}+\ldots +x_{k}^{n}= y_{1}^{n}+\ldots +y_{k}^{n}, \end{array}\right. $
где $ 1\leq x_{1},\ldots ,x_{k},y_{1},\ldots ,y_{k}\leq P$. В работе доказаны следующие теоремы.
        Теорема 1. Пусть $P>1$, $n\geq 6$, $k=n+l$. Тогда если $n$ четно и $l\leq n/2+1$, то $J_{k,n}(P) \leq e^{4,8n^{2}\ln n} P^{k+\frac{4l}{n+2}-\frac{4l}{\left( n+2\right) ^{2}}}$; если $n$ нечетно и $l\leq (n+3)/2$, то $J_{k,n}(P) \leq e^{4,8n^{2}\ln n}P^{k+\frac{4l}{n+3}}$.
        Теорема 2. Пусть $n\geq 6$. Тогда при $k=\delta n^{2}$, $1/n\leq \delta \leq 3/4$ справедлива оценка
$\displaystyle J_{k,n}\left( P\right) \leq e^{3,5n^{3}\ln n} P^{k+\left( \delta -\frac{1}{n}\right)\left( 8k-3,6n+0,72\right) }. $

Библиогр. 7.

К оглавлению номера  Go!