Вестник Московского Университета. Математика, Механика - Содержание


УДК 511.3

Омега-теорема для дзета-функции Римана вблизи прямой 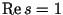${\rm Re\,}s=1$ / Зайцев С.П. // Вестн. Моск. ун-та. Сер. 1, Математика. Механика. 2000. N 3 C. 54-57.

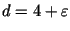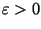Доказана следующая Теорема. Пусть $d=4+\varepsilon$, $\varepsilon>0$ -- сколь угодно малая постоянная,

\begin{displaymath} \sigma_1(t)=1-d\frac{\ln\ln\ln t}{\ln\ln t}\,, \end{displaymath}


\begin{displaymath} \Sigma(T):=\{s=\sigma+it\ \vert -T\leq t\leq T\,,\ \sigma_1(T)\leq\sigma\leq 1\}. \end{displaymath}

Тогда

\begin{displaymath} \mathop{\lim\sup}\limits_{s\in\Sigma(T),T\rightarrow\infty} \frac{\zeta(s)}{\ln T}>1. \end{displaymath}

Библиогр. 8.

К оглавлению номера  Go!