Геометрические прогрессии
Геометрической прогрессией
называется такая последовательность чисел 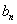 ,
что каждый следующий ее элемент получается из предыдущего умножением на некоторое
фиксированное число
,
что каждый следующий ее элемент получается из предыдущего умножением на некоторое
фиксированное число 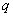 , называемое знаменателем
прогрессии.
, называемое знаменателем
прогрессии.
Приведем еще три важные формулы, касающиеся геометрической
прогрессии, которые необходимо знать наизусть:
1. Формула 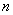 -го члена (общего
члена прогрессии)
-го члена (общего
члена прогрессии) 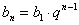 .
.
2. Формула суммы первых 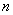 членов
прогрессии:
членов
прогрессии: 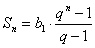 . При
. При 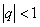 принято говорить о сходящейся геометрической прогрессии; в этом случае
можно вычислить сумму всей прогрессии по формуле
принято говорить о сходящейся геометрической прогрессии; в этом случае
можно вычислить сумму всей прогрессии по формуле 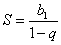 .
.
3. Формула "среднего геометрического": если 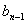 ,
,
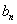 ,
, 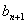 - три последовательных
члена геометрической прогрессии, то в силу определения имеем соотношения:
- три последовательных
члена геометрической прогрессии, то в силу определения имеем соотношения: 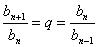 или
или 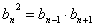 или
или 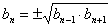 .
.
Пример 1.
Найти 4 числа, составляющие геометрическую прогрессию, в которой сумму крайних
членов равна 27, а произведение средних равно 72.
Решение. Запишем условие задачи. Имеются
четыре числа: 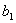 ,
, 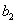 ,
,
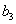 ,
, 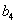 . Известно,
что
. Известно,
что 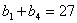 и
и 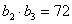 . Воспользовавшись
формулой общего члена геометрической прогрессии, получим, что
. Воспользовавшись
формулой общего члена геометрической прогрессии, получим, что 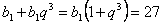 и
и 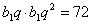 . Из второго уравнения
. Из второго уравнения  ,
что можно подставить в первое уравнение и получить:
,
что можно подставить в первое уравнение и получить: 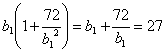 ,
откуда следует квадратное уравнение
,
откуда следует квадратное уравнение 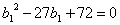 , корнями
которого являются числа 24 и 3. Находя
, корнями
которого являются числа 24 и 3. Находя 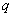 (что
очевидно), мы получим два набора чисел - первый начинается с 24:
(что
очевидно), мы получим два набора чисел - первый начинается с 24: 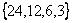 и соответствует
и соответствует 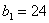 ,
, 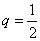 ,
второй -
,
второй - 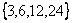 (
(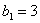 ,
,
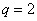 ).
).
(То, что один набор числе образует две прогрессии - со знаменателями
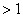 и
и 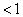 - обычная
в подобных задачах ситуация).
- обычная
в подобных задачах ситуация).
Пример 2.
Имеется шесть последовательных членов геометрической прогрессии. Сумма первых
трех в восемь раз меньше суммы последних трех. Найти знаменатель геометрической
прогрессии.
Комментарий. Поскольку прогрессия определяется двумя параметрами,
а в задаче только одно условие, мы сможем найти только знаменатель.
Решение. Запишем условие задачи:  ,
выразим все числа с помощью формулы общего члена прогрессии:
,
выразим все числа с помощью формулы общего члена прогрессии: 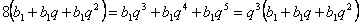 откуда после сокращения
откуда после сокращения 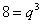 и
и 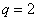 .
.
Ответ: 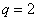 .
.
Пример 3.
В геометрической прогрессии сумма первых трех членов равна 9, а сумма первых
шести членов равна -63. Найти сумму первых десяти членов прогрессии.
Комментарий. На самом деле мы сделаем больше - мы просто
найдем и первый член - 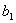 и знаменатель -
и знаменатель - 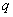 этой прогрессии. Тем самым мы, как принято говорить, "зададим" или
"построим" ее. Как результат - мы сможем найти все, что только нас
спросят про эту прогрессию, в том числе и сумму первых десяти ее членов. Заметим,
что два условия позволяют определить два параметра. Задача предлагалась абитуриентам
Воронежского Государственного Университета.
этой прогрессии. Тем самым мы, как принято говорить, "зададим" или
"построим" ее. Как результат - мы сможем найти все, что только нас
спросят про эту прогрессию, в том числе и сумму первых десяти ее членов. Заметим,
что два условия позволяют определить два параметра. Задача предлагалась абитуриентам
Воронежского Государственного Университета.
Решение. Нам пригодится то, что было проделано
в предыдущем примере. 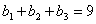 ;
; 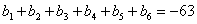 ,
откуда
,
откуда 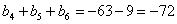 и в качестве следствия из предыдущего
примера получим
и в качестве следствия из предыдущего
примера получим 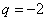 . Найдем теперь
. Найдем теперь 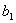 :
:
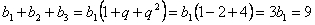 и
и 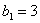 откуда окончательно:
откуда окончательно:
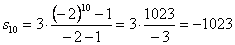 .
.
Пример 4.
Найти трехзначное число, если известно, что его цифры составляют геометрическую
прогрессию. Кроме того, если из заданного числа вычесть 297, то получится число,
записанное теми же цифрами в обратном порядке. Если к цифрам указанного числа
прибавить 8, 5 и 1, то полученные числа составят арифметическую прогрессию.
Комментарий. Задачи на числа можно зачастую решить простым
перебором. Кроме того, данный пример приводит к следующей задаче: Указать
все трехзначные числа, цифры которых образуют геометрическую прогрессию.
Замечание. Можно проверить, что последнее условие - лишнее.
Задача вполне решается и без него.
Решение. Решение перебором.
Пусть число имеет вид 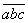 ,
где
,
где  - сотни,
- сотни, 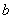 - десятки и
- десятки и 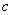 - единицы.
Для начала будем считать, что
- единицы.
Для начала будем считать, что 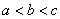 (просто потому, что числа с условием
(просто потому, что числа с условием 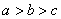 получаются автоматически "переворачиванием" тех, что мы найдем сначала).
Возможны следующие случаи -
получаются автоматически "переворачиванием" тех, что мы найдем сначала).
Возможны следующие случаи - 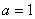 ,
тогда
,
тогда 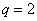 или
или 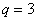 .
(поскольку
.
(поскольку 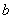 и
и 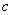 должны быть натуральными числами) Это дает нам числа 124 и 139. Кроме того,
можно заметить (подобное замечание было уже однажды сделано выше по тексты),
что числа 421 и 931 тоже подходят. Более того, число 421 удовлетворяет и второму
условию задачи, и третьему. Если к цифрам 4, 2, 1 прибавить 8, 5, 1, то получим
числа 12, 7, 2. Эти последние действительно образуют арифметическую прогрессию
с разностью
должны быть натуральными числами) Это дает нам числа 124 и 139. Кроме того,
можно заметить (подобное замечание было уже однажды сделано выше по тексты),
что числа 421 и 931 тоже подходят. Более того, число 421 удовлетворяет и второму
условию задачи, и третьему. Если к цифрам 4, 2, 1 прибавить 8, 5, 1, то получим
числа 12, 7, 2. Эти последние действительно образуют арифметическую прогрессию
с разностью 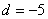 .
.
Второй возможный случай 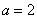 .
Тогда
.
Тогда 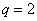 и других возможностей
нет. В этом случае
и других возможностей
нет. В этом случае 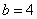 и
и
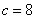 , что дает нам числа 248
и 842. Оба эти числа не подходят под условия задачи.
, что дает нам числа 248
и 842. Оба эти числа не подходят под условия задачи.
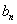 ,
что каждый следующий ее элемент получается из предыдущего умножением на некоторое
фиксированное число
,
что каждый следующий ее элемент получается из предыдущего умножением на некоторое
фиксированное число 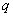 , называемое знаменателем
прогрессии.
, называемое знаменателем
прогрессии.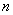 -го члена (общего
члена прогрессии)
-го члена (общего
члена прогрессии) 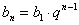 .
.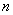 членов
прогрессии:
членов
прогрессии: 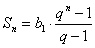 . При
. При 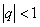 принято говорить о сходящейся геометрической прогрессии; в этом случае
можно вычислить сумму всей прогрессии по формуле
принято говорить о сходящейся геометрической прогрессии; в этом случае
можно вычислить сумму всей прогрессии по формуле 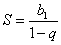 .
.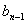 ,
,
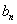 ,
, 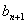 - три последовательных
члена геометрической прогрессии, то в силу определения имеем соотношения:
- три последовательных
члена геометрической прогрессии, то в силу определения имеем соотношения: 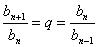 или
или 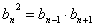 или
или 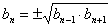 .
.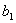 ,
, 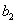 ,
,
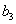 ,
, 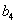 . Известно,
что
. Известно,
что 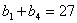 и
и 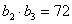 . Воспользовавшись
формулой общего члена геометрической прогрессии, получим, что
. Воспользовавшись
формулой общего члена геометрической прогрессии, получим, что 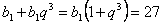 и
и 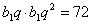 . Из второго уравнения
. Из второго уравнения  ,
что можно подставить в первое уравнение и получить:
,
что можно подставить в первое уравнение и получить: 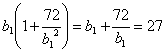 ,
откуда следует квадратное уравнение
,
откуда следует квадратное уравнение 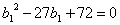 , корнями
которого являются числа 24 и 3. Находя
, корнями
которого являются числа 24 и 3. Находя 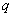 (что
очевидно), мы получим два набора чисел - первый начинается с 24:
(что
очевидно), мы получим два набора чисел - первый начинается с 24: 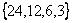 и соответствует
и соответствует 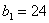 ,
, 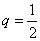 ,
второй -
,
второй - 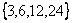 (
(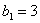 ,
,
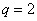 ).
).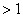 и
и 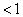 - обычная
в подобных задачах ситуация).
- обычная
в подобных задачах ситуация). ,
выразим все числа с помощью формулы общего члена прогрессии:
,
выразим все числа с помощью формулы общего члена прогрессии: 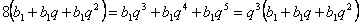 откуда после сокращения
откуда после сокращения 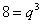 и
и 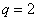 .
.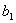 и знаменатель -
и знаменатель - 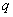 этой прогрессии. Тем самым мы, как принято говорить, "зададим" или
"построим" ее. Как результат - мы сможем найти все, что только нас
спросят про эту прогрессию, в том числе и сумму первых десяти ее членов. Заметим,
что два условия позволяют определить два параметра. Задача предлагалась абитуриентам
Воронежского Государственного Университета.
этой прогрессии. Тем самым мы, как принято говорить, "зададим" или
"построим" ее. Как результат - мы сможем найти все, что только нас
спросят про эту прогрессию, в том числе и сумму первых десяти ее членов. Заметим,
что два условия позволяют определить два параметра. Задача предлагалась абитуриентам
Воронежского Государственного Университета.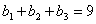 ;
; 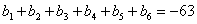 ,
откуда
,
откуда 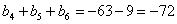 и в качестве следствия из предыдущего
примера получим
и в качестве следствия из предыдущего
примера получим 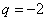 . Найдем теперь
. Найдем теперь 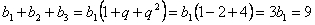 и
и 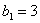 откуда окончательно:
откуда окончательно:
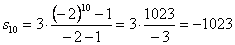 .
. 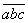 ,
где
,
где  - сотни,
- сотни, 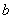 - десятки и
- десятки и 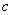 - единицы.
Для начала будем считать, что
- единицы.
Для начала будем считать, что 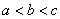 (просто потому, что числа с условием
(просто потому, что числа с условием 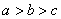 получаются автоматически "переворачиванием" тех, что мы найдем сначала).
Возможны следующие случаи -
получаются автоматически "переворачиванием" тех, что мы найдем сначала).
Возможны следующие случаи - 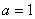 ,
тогда
,
тогда 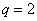 или
или 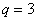 .
(поскольку
.
(поскольку 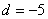 .
.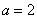 .
Тогда
.
Тогда 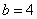 и
и
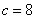 , что дает нам числа 248
и 842. Оба эти числа не подходят под условия задачи.
, что дает нам числа 248
и 842. Оба эти числа не подходят под условия задачи.