Корни многочленов
Многочлен от
переменной 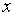 можно рассматривать как функцию от
можно рассматривать как функцию от 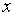 .
А именно, значением многочлена
.
А именно, значением многочлена 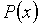 в точке
в точке 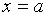 называется число, получающееся при
подстановке в выражение для
называется число, получающееся при
подстановке в выражение для 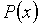 вместо символа
вместо символа 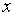 числа
числа 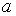 (и
выполнения соответствующих арифметических
операций). Например, значение многочлена
(и
выполнения соответствующих арифметических
операций). Например, значение многочлена 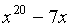 в точке
в точке 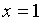 равно
равно 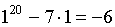 .
.
Те значения переменной 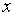 ,
при которых выполняется равенство
,
при которых выполняется равенство 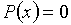 ,
называются корнями многочлена
,
называются корнями многочлена 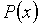 .
Графически корнями многочлена
.
Графически корнями многочлена 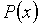 являются абсциссы пересечения графика
функции
являются абсциссы пересечения графика
функции 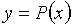 с осью абсцисс.
с осью абсцисс.
Остановимся подробнее на задаче
отыскания корней многочлена.
Многочленом нулевой степени
является любое отличное от нуля число.
Корней такой многочлен не имеет.
Общим видом многочлена первой
степени является выражение вида 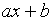 ,
где
,
где 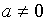 .
Этот многочлен имеет ровно один корень
.
Этот многочлен имеет ровно один корень 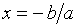 .
.
Многочлен второй степени 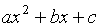 (
(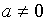 )
называется квадратным трехчленом, а число
)
называется квадратным трехчленом, а число 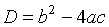 - дискриминантом этого квадратного
трехчлена.
- дискриминантом этого квадратного
трехчлена.
Теорема 1. Если
дискриминант 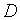 квадратного трехчлена
квадратного трехчлена 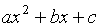 положителен, то этот трехчлен имеет ровно
два (различных) корня
положителен, то этот трехчлен имеет ровно
два (различных) корня 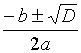 .
Если
.
Если 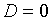 , то
существует в точности один корень, равный
, то
существует в точности один корень, равный  .
В случае
.
В случае 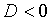 рассматриваемый трехчлен корней не имеет.
рассматриваемый трехчлен корней не имеет.
Пример
2.1. Найти число корней уравнения  при каждом значении параметра
при каждом значении параметра 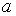 .
.
РЕШЕНИЕ. Требуется найти число
корней многочлена 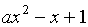 .
При
.
При 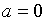 это
многочлен первой степени
это
многочлен первой степени 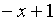 ,
число корней которого равно
,
число корней которого равно 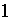 .
Если же
.
Если же 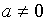 ,
то мы имеем дело с квадратным трехчленом и
можем применить теорему о числе его корней
в зависимости от знака дискриминанта.
Поскольку
,
то мы имеем дело с квадратным трехчленом и
можем применить теорему о числе его корней
в зависимости от знака дискриминанта.
Поскольку 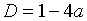 ,
мы заключаем, что при
,
мы заключаем, что при 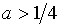 корней нет, при
корней нет, при 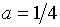 корень ровно один, а при
корень ровно один, а при 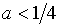 (и
(и 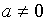 )
рассматриваемый трехчлен имеет ровно два
корня.
)
рассматриваемый трехчлен имеет ровно два
корня.
ОТВЕТ: при 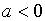 и
и 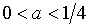 имеются
имеются 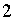 корня, при
корня, при 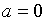 и
и 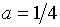 - один,
а при
- один,
а при 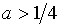 корней нет.
корней нет.
Часто для
того, чтобы показать отсутствие корней у
заданного трехчлена, бывает удобно
выделить в нем полный квадрат. Метод
выделения полного квадрата полезен и при
решении ряда других задач.
Пример 2.2.
Найти наибольшее значение квадратного
трехчлена  .
.
РЕШЕНИЕ. Поскольку 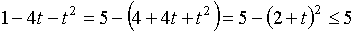 ,
причем неравенство обращается в равенство
при
,
причем неравенство обращается в равенство
при 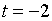 , мы
заключаем, что наибольшее значение
заданного квадратного трехчлена равно
, мы
заключаем, что наибольшее значение
заданного квадратного трехчлена равно 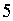 .
.
ОТВЕТ: 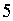 .
.
Связь между
корнями квадратного трехчлена и его
коэффициентами раскрывается в следующем
утверждении.
Теорема 2 (Ф.
Виет). Если 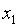 и
и  - корни
приведенного квадратного трехчлена
- корни
приведенного квадратного трехчлена  ,
то
,
то 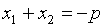 и
и  .
.
Обратно, ели некоторые числа 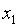 и
и  удовлетворяют последним двум равенствам,
то эти числа являются корнями квадратного
трехчлена
удовлетворяют последним двум равенствам,
то эти числа являются корнями квадратного
трехчлена  .
.
Теорема
Виета и обратная к ней позволяют быстро
раскладывать квадратные трехчлены на
множители и находить их корни. В частности,
можно устно решать некоторые квадратные
уравнения, не прибегая к формуле корней.
Пример 2.3. Решить
уравнение  .
.
РЕШЕНИЕ. Произведение корней
равно 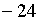 , а
их сумма
, а
их сумма 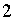 .
Ясно, что корнями являются числа
.
Ясно, что корнями являются числа 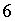 и
и 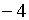 .
.
ОТВЕТ: 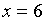 и
и 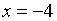 .
.
Пример 2.4. Разложить
на множители трехчлен 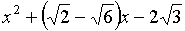 .
.
РЕШЕНИЕ. Заметим, что 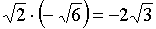 ,
так что искомое разложение имеет вид
,
так что искомое разложение имеет вид 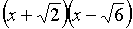 .
.
ОТВЕТ: 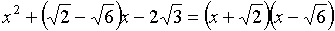 .
.
Пример 2.5. Найдите
все пары чисел 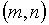 ,
удовлетворяющие условиям
,
удовлетворяющие условиям  и
и 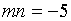 .
.
РЕШЕНИЕ. Как мы знаем, искомые
числа 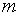 и
и 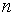 являются корнями некоторого (вполне
определенного) квадратного уравнения.
Можно составить это уравнение и решить, но
мы поступим по-иному. Ввиду того, что всякий
квадратный трехчлен имеет не более двух
корней, наша задача не может иметь более
двух решений, поэтому нам достаточно
предъявить две пары чисел
являются корнями некоторого (вполне
определенного) квадратного уравнения.
Можно составить это уравнение и решить, но
мы поступим по-иному. Ввиду того, что всякий
квадратный трехчлен имеет не более двух
корней, наша задача не может иметь более
двух решений, поэтому нам достаточно
предъявить две пары чисел 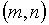 ,
удовлетворяющих условиям
,
удовлетворяющих условиям  и
и 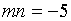 .
.
ОТВЕТ: 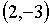 и
и 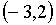 .
.
Теорему Виета
можно применять и в более общем случае,
когда старший коэффициент квадратного
уравнения отличен от единицы. Для этого все
коэффициенты трехчлена почленно делят на
старший, получая приведенный квадратный
трехчлен с теми же корнями, что и у
исходного.
Пример 2.6. Не
вычисляя корней уравнения  ,
найти сумму их квадратов.
,
найти сумму их квадратов.
РЕШЕНИЕ. Пусть 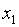 и
и 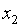 - корни
этого уравнения. Они являются корнями
приведенного квадратного трехчлена
- корни
этого уравнения. Они являются корнями
приведенного квадратного трехчлена 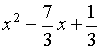 ,
поэтому
,
поэтому 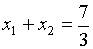 ,
а
,
а 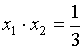 .
Следовательно,
.
Следовательно,  .
.
ОТВЕТ: 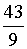 .
.
В ряде
случаев один из корней квадратного
трехчлена можно угадать. Тогда второй
корень можно найти, используя теорему Виета.
Пример 2.7. Решить
устно уравнение 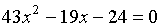 .
.
РЕШЕНИЕ. Заметим, что 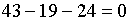 ,
так что единица является корнем. Поскольку
произведение корней равно
,
так что единица является корнем. Поскольку
произведение корней равно  ,
этому числу и равен второй корень исходного
уравнения.
,
этому числу и равен второй корень исходного
уравнения.
ОТВЕТ: 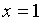 и
и 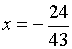 .
.
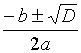 .
Если
.
Если  .
.