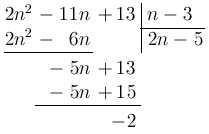Определения и
основные факты
Многочленом степени
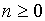 от переменной
от переменной 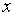 называется алгебраическое выражение вида
называется алгебраическое выражение вида 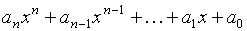 ,
где
,
где 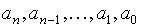 -
некоторые числа, называемые коэффициентами
многочлена, причем
-
некоторые числа, называемые коэффициентами
многочлена, причем 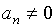 .
.
Например, 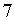 - многочлен нулевой степени, а
- многочлен нулевой степени, а 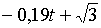 - многочлен первой степени от переменной
- многочлен первой степени от переменной 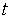 .
.
На множестве многочленов можно
очевидным способом определить операции
сложения, вычитания и умножения. Например,
суммой многочленов 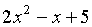 и
и 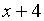 является многочлен
является многочлен 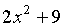 ,
а произведением многочленов
,
а произведением многочленов 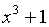 и
и 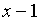 -
многочлен
-
многочлен 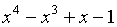 .
Однако не каждый многочлен можно разделить
на другой нацело, то есть для данных
многочленов
.
Однако не каждый многочлен можно разделить
на другой нацело, то есть для данных
многочленов 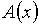 и
и 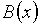 не
всегда можно найти такой многочлен
не
всегда можно найти такой многочлен 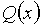 ,
что
,
что 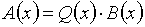 . К
примеру, невозможно разделить нацело
многочлен
. К
примеру, невозможно разделить нацело
многочлен 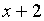 на многочлен
на многочлен 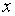 .
Но, как и для целых чисел, можно сказать, что
поскольку
.
Но, как и для целых чисел, можно сказать, что
поскольку 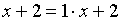 ,
то (неполным) частным от деления
,
то (неполным) частным от деления 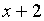 на
на 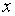 является многочлен
является многочлен 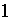 ,
а остатком - многочлен
,
а остатком - многочлен 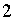 .
Итак, введем строгое определение.
.
Итак, введем строгое определение.
Разделить многочлен 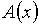 на многочлен
на многочлен 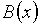 с остатком означает найти два таких
многочлена
с остатком означает найти два таких
многочлена 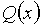 и
и 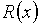 , что
, что 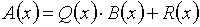 ,
причем степень многочлена
,
причем степень многочлена 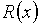 должна быть меньше степени многочлена
должна быть меньше степени многочлена 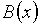 .
.
Последнее условие аналогично
требованию, чтобы остаток от деления на
число не превосходил самого этого числа.
Как и в случае деления с остатком целых
чисел, деление многочленов может быть также
выполнено "столбиком".
Пример 1.1. Разделить
с остатком многочлен 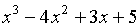 на многочлен
на многочлен 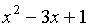 .
.
РЕШЕНИЕ. Воспользуемся делением
"столбиком":
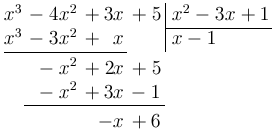
ОТВЕТ: 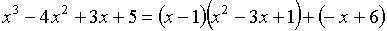 .
.
Деление
многочленов с остатком может быть полезно
при решении задач, связанных со свойствами
целых чисел.
Пример 1.2. При
каких натуральных значениях 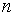 выражение
выражение 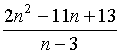 является целым числом?
является целым числом?
РЕШЕНИЕ. Разделим числитель
дроби на знаменатель с остатком:
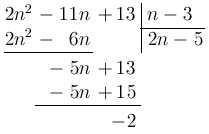
Таким образом, исходное
выражение равно 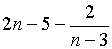 ,
что является целым числом тогда и только
тогда, когда
,
что является целым числом тогда и только
тогда, когда 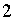 нацело делится на
нацело делится на 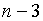 .
Поскольку целыми делителями числа
.
Поскольку целыми делителями числа 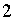 являются числа
являются числа 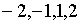 и только они, получаем
и только они, получаем
ОТВЕТ: 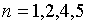 .
.
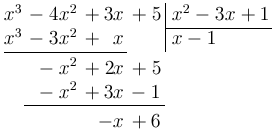
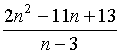 является целым числом?
является целым числом?