Случай многих модулей
В этом параграфе мы рассмотрим более сложные задачи, для решения которых можно применить метод, схожий с методом интервалов.
Пример 3.1. Решить
уравнение ![]() .
.
![]()
РЕШЕНИЕ. Изобразим на числовой оси все
точки, в которых хотя бы одно из выражений,
стоящих под модулем, меняет знак. Отметим,
что выражение ![]() меняет знак в точке
меняет знак в точке ![]() .
Мы видим, что при
.
Мы видим, что при ![]() все три модуля раскроются "с минусом",
при
все три модуля раскроются "с минусом",
при ![]() первый модуль раскроется "с плюсом", а
остальные два - "с минусом" и т.д.
Рассмотрим каждый из получившихся четырех
случаев.
первый модуль раскроется "с плюсом", а
остальные два - "с минусом" и т.д.
Рассмотрим каждый из получившихся четырех
случаев.


Собирая вместе все результаты, получаем
ОТВЕТ: ![]() .
.
Отметим, что если бы мы раскрывали каждый модуль по отдельности, нам пришлось бы рассмотреть не четыре, а восемь случаев. Рассмотрим еще один пример подобной экономии времени и сил.
Пример
3.2. Решить неравенство ![]() .
.
![]()
РЕШЕНИЕ. Изобразим на числовой оси все точки, в которых хотя бы одно из выражений, стоящих под модулем, меняет знак. Рассмотрим каждый из получившихся трех (а не четырех) случаев.
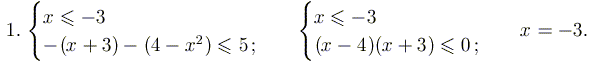
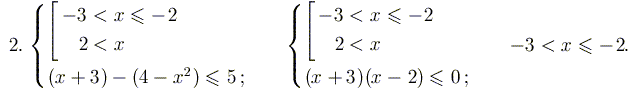
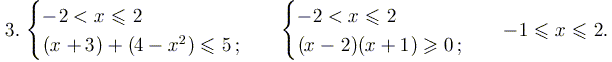
Собирая вместе все результаты, получаем
ОТВЕТ: ![]() ,
,
![]() .
.
Задачи этого раздела предполагают использование как приемов, изложенных в настоящем параграфе, так и методов, рассмотренных ранне.