
Способы раскрытия модулей
Приведем несколько теорем, которые полезно использовать при решении задач.
Теорема 3. 
Теорема 4. ![]() .
.
Пример 2.1. Решить
уравнение ![]() .
.
РЕШЕНИЕ.
I. (Геометрический
подход.) Поскольку ![]() ,
нам нужно найти на числовой оси все точки
,
нам нужно найти на числовой оси все точки ![]() ,
расстояние от которых до точки
,
расстояние от которых до точки ![]() равно
равно ![]() .
Ясно. что этих точек две:
.
Ясно. что этих точек две: ![]() и
и ![]() .
.
![]()
II. (Алгебраический подход.) По теореме 3
имеем ![]() или
или ![]() .
.
ОТВЕТ: ![]() ,
,
![]() .
.
Пример 2.2. Решить
уравнение ![]() .
.
РЕШЕНИЕ. I. (Геометрический подход.)
Поскольку ![]() ,
нам нужно найти на числовой оси все точки
,
нам нужно найти на числовой оси все точки ![]() ,
расстояние от которых до точки
,
расстояние от которых до точки ![]() равно расстоянию до точки
равно расстоянию до точки ![]() .
Ясно, что левее
.
Ясно, что левее ![]() и правее
и правее ![]() таких точек нет. Значит, круг поисков
сужается до отрезка
таких точек нет. Значит, круг поисков
сужается до отрезка ![]() ,
а так как из всех точек отрезка от его
концов равноудалена лишь середина, мы
получаем единственную точку
,
а так как из всех точек отрезка от его
концов равноудалена лишь середина, мы
получаем единственную точку ![]() .
.
![]()
II. (Алгебраический
подход.) По теореме 4 имеем ![]() или
или ![]() .
Последнее уравнение решений не имеет,
поэтому получаем
.
Последнее уравнение решений не имеет,
поэтому получаем
ОТВЕТ: ![]() .
.
Геометрический подход бывает полезен для
устного решения поставленной задачи, а
также для наглядности производимых с
модулем действий. При этом можно считать,
что действительное число и изображающая
его точка на числовой прямой - одно и то же. В
свою очередь, алгебраический подход
является предпочтительным при оформлении
письменных работ.
В случае если уравнение содержит
несколько выражений под модулем, например,
имеет вид ![]() ,
целесообразно разбить числовую ось на
промежутки, на которых каждое выражение,
стоящее под модулем, сохраняет знак. Это
разбиение определяется точками, в которых
стоящие под модулями выражения обращаются
в нуль.
,
целесообразно разбить числовую ось на
промежутки, на которых каждое выражение,
стоящее под модулем, сохраняет знак. Это
разбиение определяется точками, в которых
стоящие под модулями выражения обращаются
в нуль.
Пример
2.3. Решить уравнение ![]() .
.
РЕШЕНИЕ. I. (Геометрический подход.)
В задаче требуется найти все точки на
числовой оси, сумма расстояний от каждой из
которых до точек ![]() и
и ![]() равна
равна ![]() .
Изобразим эти точки на числовой оси. Если
точка
.
Изобразим эти точки на числовой оси. Если
точка ![]() лежит на отрезке
лежит на отрезке ![]() ,
то сумма расстояний от нее до точек
,
то сумма расстояний от нее до точек ![]() и
и ![]() равна
длине отрезка
равна
длине отрезка ![]() ,
то есть
,
то есть ![]() .
Следовательно, искомые точки
.
Следовательно, искомые точки ![]() не могут располагаться на отрезке
не могут располагаться на отрезке ![]() .
.
![]()
Пусть теперь точка ![]() лежит левее точки
лежит левее точки ![]() .
Тогда сумма расстояний от точки
.
Тогда сумма расстояний от точки ![]() до точек
до точек ![]() и
и ![]() равно
сумме удвоенного расстояния от точки
равно
сумме удвоенного расстояния от точки ![]() до точки
до точки ![]() и длины отрезка
и длины отрезка ![]() .
Поскольку эта сумма по условию равна
.
Поскольку эта сумма по условию равна ![]() ,
мы получаем, что расстояние от точки
,
мы получаем, что расстояние от точки ![]() до точки
до точки ![]() равно
равно ![]() , а
значит,
, а
значит, ![]() .
.
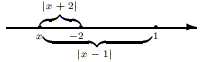
Случай, когда точка ![]() лежит правее точки
лежит правее точки ![]() ,
рассматривается аналогично. Впрочем, можно
сказать, что в силу симметрии условия
относительно центра отрезка
,
рассматривается аналогично. Впрочем, можно
сказать, что в силу симметрии условия
относительно центра отрезка ![]() в оставшемся случае расстояние от точки
в оставшемся случае расстояние от точки ![]() до точки
до точки ![]() будет также равно
будет также равно ![]() ,
поэтому еще одним решением нашей задачи
является
,
поэтому еще одним решением нашей задачи
является ![]() .
Ясно, что других решений нет.
.
Ясно, что других решений нет.
II. (Алгебраический подход.)
Рассмотрим три случая.
Собирая вместе все результаты, получаем
ОТВЕТ: ![]() ,
,
![]() .
.
Проведенные геометрические рассуждения
позволяют установить, что корни уравнения ![]() заполняют отрезок
заполняют отрезок ![]() ,
а, например, уравнение
,
а, например, уравнение ![]() корней не имеет. Вообще, справедливо такое
утверждение.
корней не имеет. Вообще, справедливо такое
утверждение.
Теорема
5. Уравнение ![]() ,
где
,
где ![]() ,
,
1) имеет два корня, если ![]() ;
;
2) имеет решением отрезок ![]() ,
если
,
если ![]() ;
;
3) не имеет корней при ![]() .
.
Разумеется, запоминать этот факт вовсе не обязательно; достаточно понять его смысл, например, представив себе геометрические картинки, соответствующие различным случаям этого утверждения.
Пример
2.4. Решить неравенство ![]() .
.
РЕШЕНИЕ. I. (Геометрический подход.)
В задаче требуется найти все точки на
числовой оси, разность расстояний от каждой
из которых до точек ![]() и
и ![]() не
превосходит
не
превосходит ![]() .
Изобразим эти точки на числовой оси.
.
Изобразим эти точки на числовой оси.
Пусть сначала точка ![]() лежит правее точки
лежит правее точки ![]() .
Тогда рассматриваемая разность равна длине
отрезка
.
Тогда рассматриваемая разность равна длине
отрезка ![]() ,
то есть семи, что больше единицы.
,
то есть семи, что больше единицы.
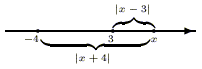
Пусть теперь точка ![]() лежит левее точки
лежит левее точки ![]() .
Тогда рассматриваемая разность расстояний
равна
.
Тогда рассматриваемая разность расстояний
равна ![]() , а
следовательно, все такие точки
удовлетворяют нашему неравенству.
, а
следовательно, все такие точки
удовлетворяют нашему неравенству.
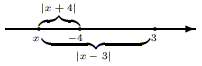
Пусть, наконец, точка ![]() лежит на отрезке
лежит на отрезке ![]() .
Заметим, что при движении точки
.
Заметим, что при движении точки ![]() по этому отрезку от
по этому отрезку от ![]() до
до ![]() рассматриваемая разность расстояний
возрастает от
рассматриваемая разность расстояний
возрастает от ![]() до
до ![]() ,
причем равна
,
причем равна ![]() лишь при
лишь при ![]() (здесь можно решить систему
(здесь можно решить систему ![]() ,
,
![]() , где
, где ![]() и
и ![]() -
расстояния от точки
-
расстояния от точки ![]() до концов отрезка). Таким образом, получаем,
что все решения исходного неравенства
заполняют луч
до концов отрезка). Таким образом, получаем,
что все решения исходного неравенства
заполняют луч ![]() .
.
II. (Алгебраический подход.)
Рассмотрим три случая.
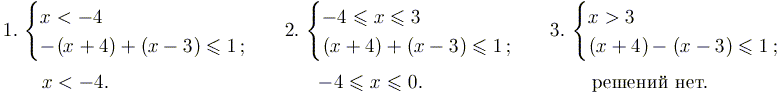
Собирая вместе все результаты, получаем
ОТВЕТ: ![]() .
.
Еще раз подчеркнем, что геометрическая интерпретация привносит наглядность в решение задачи. Конечно, приводимые алгебраические выкладки менее длинны и более привлекательны, но, тем не менее, иногда бывает полезно и представить себе, как выглядит рассматриваемое множество на числовой прямой. Например, проведенные геометрические рассуждения позволяют установить следующий факт.
Теорема
6. При всех действительных значениях
справедливо двойное неравенство ![]() ,
причем если
,
причем если ![]() ,
то
,
то
1) левое неравенство обращается в
равенство ![]() ;
;
2) правое неравенство обращается
в равенство ![]() .
.
К задач этого раздела полезно применить и алгебраический, и геометрический подходы.