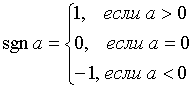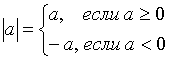Определения и
основные факты
Понятие
модуля, или абсолютного значения,
действительного числа допускает несколько
подходов. Мы начнем с геометрического
истолкования этого понятия.
Как известно, каждое
действительное число можно отождествить с
точкой на числовой прямой. Поскольку про
каждую отличную от нуля точку можно сказать,
лежит она левее нуля или правее, а также
измерить расстояние от этой точки до нуля,
мы можем связать с каждым действительным
числом две величины: его знак и его модуль. А
именно, если точка, изображающая число 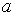 ,
лежит левее нуля, то говорят, что знак числа
,
лежит левее нуля, то говорят, что знак числа 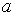 отрицателен, а если правее нуля, то говорят,
что знак числа
отрицателен, а если правее нуля, то говорят,
что знак числа 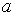 положителен; число
положителен; число 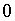 знака не имеет. Модуль числа
знака не имеет. Модуль числа 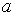 ,
равный расстоянию от точки, изображающей
число
,
равный расстоянию от точки, изображающей
число 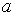 ,
до нуля можно измерить для всех
действительных чисел. Например, число
,
до нуля можно измерить для всех
действительных чисел. Например, число 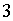 положительно, а его модуль равен
положительно, а его модуль равен 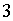 ,
число
,
число 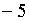 отрицательно, а его модуль равен
отрицательно, а его модуль равен 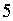 ;
модуль нуля равен нулю. Как мы видим, модуль
положительного числа равен самому этому
числа. Модуль отрицательного числа равен
"минус"-этому числу, то есть
противоположному числу; например, модуль
числа
;
модуль нуля равен нулю. Как мы видим, модуль
положительного числа равен самому этому
числа. Модуль отрицательного числа равен
"минус"-этому числу, то есть
противоположному числу; например, модуль
числа 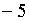 равен
равен 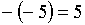 .
Таким образом, каждое действительно число
.
Таким образом, каждое действительно число 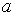 можно записать в виде
можно записать в виде 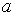 =знак
=знак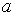 модуль
модуль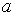 .
Более точно, вводятся две функции
действительного аргумента
.
Более точно, вводятся две функции
действительного аргумента 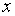 ,
называемые знаком и модулем:
,
называемые знаком и модулем: 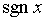 и
и  соответственно (signum - знак (лат.)). По
определению полагают
соответственно (signum - знак (лат.)). По
определению полагают
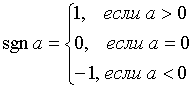
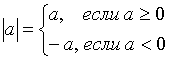
Итак, отталкиваясь от
геометрической интерпретации
действительного числа. мы пришли к ъорошо
известному алгебраическому определению
модуля.
Теорема
1. Во введенных обозначениях имеют место
тождества 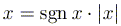 и
и 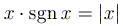 .
.
Дальнейшее утверждение
перечисляет свойства модуля, а также
раскрывает связь между модулем и
арифметическими, а также алгебраическими
операциями. Отметим, что значение 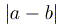 равно расстоянию на числовой прямой между
точками, изображающими числа
равно расстоянию на числовой прямой между
точками, изображающими числа 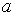 и
и 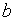 .
.
Теорема 2. Следующие
свойства справедливы для всех
действительных значений входящих в них
переменных.
1) 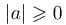 ,
причем
,
причем 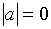 тогда и только тогда, когда
тогда и только тогда, когда 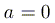 .
.
2) 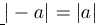 .
.
3) 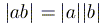 ;
в частности,
;
в частности, 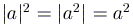 .
.
4) 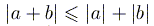 ;
;
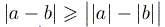 .
.
5) 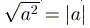 .
.
6) 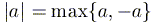 ;
в частности
;
в частности 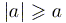 и
и 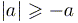 .
.
Пример
1.1. Решить уравнение 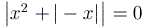 .
.
РЕШЕНИЕ. Преобразуем левую часть
уравнения: 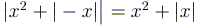 .
Поскольку каждое из полученных слагаемых
неотрицательно при всех значениях
.
Поскольку каждое из полученных слагаемых
неотрицательно при всех значениях 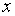 ,
рассматриваемая сумма также всегда
неотрицательно, причем равна нулю тогда и
только тогда, когда каждое из слагаемых
равно нулю. Таким образом, исходное
уравнение равносильно уравнению
,
рассматриваемая сумма также всегда
неотрицательно, причем равна нулю тогда и
только тогда, когда каждое из слагаемых
равно нулю. Таким образом, исходное
уравнение равносильно уравнению 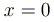 .
.
ОТВЕТ: 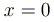 .
.
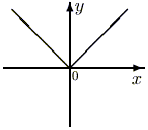
Графики
функций 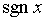 и
и  выглядят следующим образом. Функция
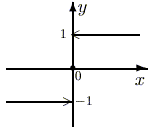
выглядят следующим образом. Функция 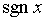 разрывна в нуле и нечетна. Функция
разрывна в нуле и нечетна. Функция  непрерывна на всей числовой прямой и четна.
При отрицательных значениях переменной она
убывает. а при положительных - возрастает.
непрерывна на всей числовой прямой и четна.
При отрицательных значениях переменной она
убывает. а при положительных - возрастает.
Пример
1.2. При каждом значении параметра 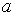 найти число точек пересечения кривых
найти число точек пересечения кривых 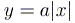 и
и 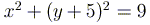 .
.
РЕШЕНИЕ. Изобразим на плоскости  данные кривые. первая из них получается с
помощью сжатия и, быть может, симметрии
относительно оси
данные кривые. первая из них получается с
помощью сжатия и, быть может, симметрии
относительно оси 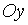 графика функции
графика функции 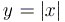 ,
а второе уравнение задает окружность
радиуса
,
а второе уравнение задает окружность
радиуса 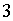 с центром в точке
с центром в точке 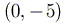 .
При
.
При 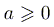 кривая
кривая 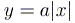 лежит в первой и второй четвертях включая
ось
лежит в первой и второй четвертях включая
ось 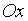 (при
(при 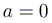 кривая
кривая 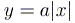 совпадает с осью
совпадает с осью 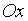 ),
а окружность
),
а окружность 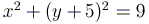 - в третьей и четвертой, не имея общих точек
с осью
- в третьей и четвертой, не имея общих точек
с осью 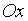 .
Следовательно, в этом случае данные кривые
не пересекаются.
.
Следовательно, в этом случае данные кривые
не пересекаются.
Пусть теперь 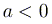 .
При малых по модулю значениях параметра
.
При малых по модулю значениях параметра 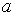 у рассматриваемых кривых общих точек по-прежнему
не будет. Затем при уменьшении параметра
у рассматриваемых кривых общих точек по-прежнему
не будет. Затем при уменьшении параметра 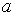 ,
произойдет касание (этот момент изображен
на рисунке),
,
произойдет касание (этот момент изображен
на рисунке),
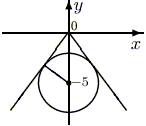
а при всех
меньших значениях этого параметра будет
ровно четыре общие точки. Остается лишь
найти то значение параметра 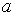 ,
при котором произойдет касание. Проведя
радиус, получим египетский треугольник (то
есть треугольник со сторонами
,
при котором произойдет касание. Проведя
радиус, получим египетский треугольник (то
есть треугольник со сторонами 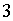 ,
,
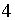 ,
, 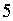 ),
из которого нетрудно найти угловой
коэффициент соответствующей полупрямой:
),
из которого нетрудно найти угловой
коэффициент соответствующей полупрямой: 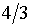 .
.
ОТВЕТ: При 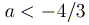 число точек пересечения равно четырем, при
число точек пересечения равно четырем, при 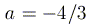 - двум. а при
- двум. а при 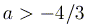 точки пересечения отсутствуют.
точки пересечения отсутствуют.
Пример
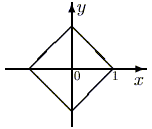
1.3. Какая геометрическая фигура задается
уравнением 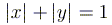 ?
Сделать чертеж.
?
Сделать чертеж.
РЕШЕНИЕ. Нетрудно видеть, что
вместе с каждой своей точкой 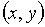 наша фигура содержит также точки
наша фигура содержит также точки 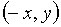 ,
,
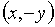 ,
, 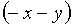 .
Значит, нам достаточно изобразить часть
этой фигуры, лежащую в первой четверти, а
затем отразить полученную кривую
относительно обеих осей и начала координат.
.
Значит, нам достаточно изобразить часть
этой фигуры, лежащую в первой четверти, а
затем отразить полученную кривую
относительно обеих осей и начала координат.
Итак, пусть 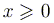 и
и 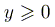 . Тогда
исходное уравнение принимает вид
. Тогда
исходное уравнение принимает вид 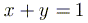 .
Значит, лежащей в первой четверти частью
фигуры является соответствующий отрезок
прямой
.
Значит, лежащей в первой четверти частью
фигуры является соответствующий отрезок
прямой 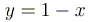 .
произведя все указанные отражения этого
отрезка, получим четырехугольник с равными
перпендикулярными диагоналями, то есть
квадрат.
.
произведя все указанные отражения этого
отрезка, получим четырехугольник с равными
перпендикулярными диагоналями, то есть
квадрат.
ОТВЕТ: квадрат.