Логарифмические неравенства
Пример
3.1. 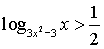 - простая по
идее решения, но требующая достаточных
технических усилий задача. Необходимо, как
и раньше, учесть условия на основание (оно
должно быть больше нуля и не равно 1), на сам
- простая по
идее решения, но требующая достаточных
технических усилий задача. Необходимо, как
и раньше, учесть условия на основание (оно
должно быть больше нуля и не равно 1), на сам 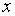 (он также
(он также 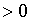 ) и не
забыть рассмотреть два случая - когда
основание
) и не
забыть рассмотреть два случая - когда
основание 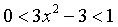 и когда
и когда 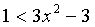 .
.
РЕШЕНИЕ:
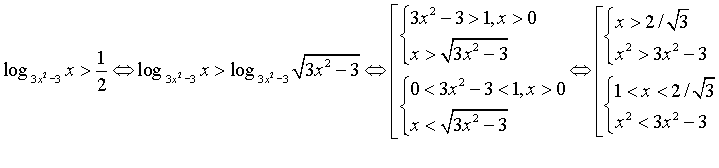
Вторая
система не имеет решения, а первая дает нам
ответ: 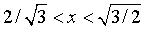 . Заметим, что
возводя в квадрат неравенства
. Заметим, что
возводя в квадрат неравенства 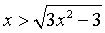 и
и 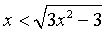 , мы пользовались
условием
, мы пользовались
условием 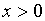 .
.
ОТВЕТ: 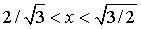 .
.
Пример
3.2. 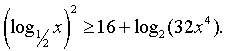 - Здесь сначала нужно
привести неравенство к «обычному»
квадратичному виду, после чего решить это
неравенство и окончательно «разобраться» с
логарифмами.
- Здесь сначала нужно
привести неравенство к «обычному»
квадратичному виду, после чего решить это
неравенство и окончательно «разобраться» с
логарифмами.
РЕШЕНИЕ: Вспомнив свойства
логарифма, получим: 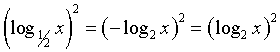 ,
, 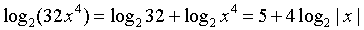 .
Наше неравенство превращается в следующее:
.
Наше неравенство превращается в следующее: 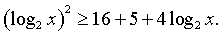 Модуль можно опустить, поскольку выражение
в левой части логарифма определено лишь при
Модуль можно опустить, поскольку выражение
в левой части логарифма определено лишь при
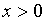 . Сделав замену
переменных
. Сделав замену
переменных 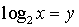 ,
получаем неравенство
,
получаем неравенство 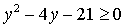 ,
решением которого будет
,
решением которого будет 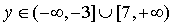 .
Произведя обратную замену получаем ответ:
.
Произведя обратную замену получаем ответ: 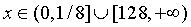 .
.
ОТВЕТ: 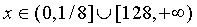 .
.
Пример
3.3. 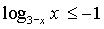 - простая по
идеологии, но трудоемкая в реализации
задача.
- простая по
идеологии, но трудоемкая в реализации
задача.
РЕШЕНИЕ:
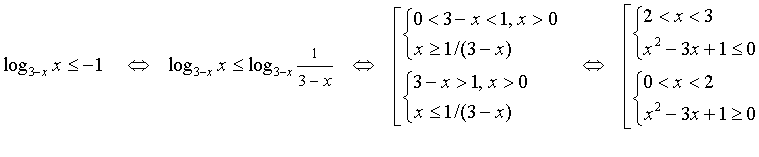
Из
первой системы имеем 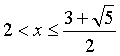 ,
а из второй -
,
а из второй - 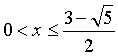 . Таким
образом, получаем ответ:
. Таким
образом, получаем ответ: 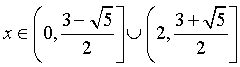 .
.
ОТВЕТ: 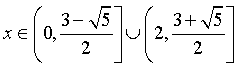 .
.
Пример
3.4. 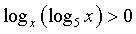 .
.
РЕШЕНИЕ: Рассмотрим 2 случая.
Первый, когда 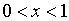 , и
второй, когда
, и
второй, когда 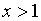 .
.
1) 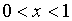 . При
этих значениях
. При
этих значениях 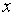 ,
, 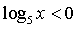 и тогда левая часть не определена. То есть
ни одно значение
и тогда левая часть не определена. То есть
ни одно значение 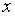 интервала
интервала 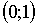 не входит
в решение.
не входит
в решение.
2) 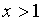 . Наше
неравенство эквивалентно следующему:
. Наше
неравенство эквивалентно следующему: 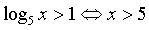 ,
что в совокупности с условием
,
что в совокупности с условием 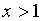 ,
дает промежуток решения
,
дает промежуток решения 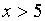 .
.
ОТВЕТ: 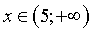 .
.
Пример
3.5. 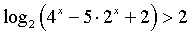 .
.
РЕШЕНИЕ: 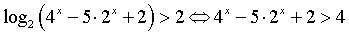 .
Далее заменяем
.
Далее заменяем 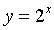 и
приходим к неравенству
и
приходим к неравенству 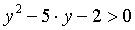 ,
что в совокупности с условием
,
что в совокупности с условием 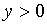 дает
дает 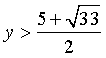 . Делаем
обратную замену:
. Делаем
обратную замену: 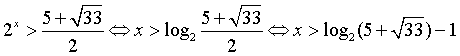 .
.
ОТВЕТ: 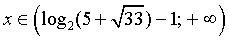 .
.
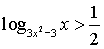 - простая по
идее решения, но требующая достаточных
технических усилий задача. Необходимо, как
и раньше, учесть условия на основание (оно
должно быть больше нуля и не равно 1), на сам
- простая по
идее решения, но требующая достаточных
технических усилий задача. Необходимо, как
и раньше, учесть условия на основание (оно
должно быть больше нуля и не равно 1), на сам 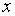 (он также
(он также 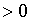 ) и не
забыть рассмотреть два случая - когда
основание
) и не
забыть рассмотреть два случая - когда
основание 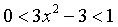 и когда
и когда 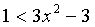 .
.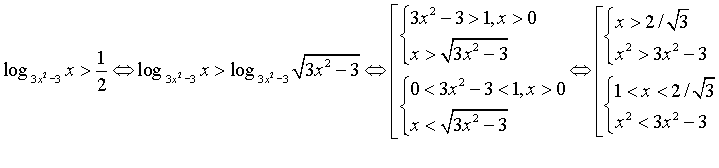
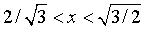 . Заметим, что
возводя в квадрат неравенства
. Заметим, что
возводя в квадрат неравенства 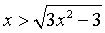 и
и 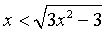 , мы пользовались
условием
, мы пользовались
условием 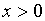 .
.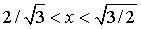 .
.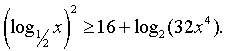 - Здесь сначала нужно
привести неравенство к «обычному»
квадратичному виду, после чего решить это
неравенство и окончательно «разобраться» с
логарифмами.
- Здесь сначала нужно
привести неравенство к «обычному»
квадратичному виду, после чего решить это
неравенство и окончательно «разобраться» с
логарифмами.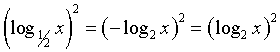 ,
, 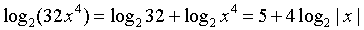 .
Наше неравенство превращается в следующее:
.
Наше неравенство превращается в следующее: 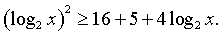 Модуль можно опустить, поскольку выражение
в левой части логарифма определено лишь при
Модуль можно опустить, поскольку выражение
в левой части логарифма определено лишь при
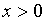 . Сделав замену
переменных
. Сделав замену
переменных 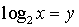 ,
получаем неравенство
,
получаем неравенство 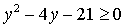 ,
решением которого будет
,
решением которого будет 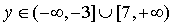 .
Произведя обратную замену получаем ответ:
.
Произведя обратную замену получаем ответ: 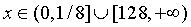 .
.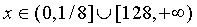 .
.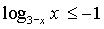 - простая по
идеологии, но трудоемкая в реализации
задача.
- простая по
идеологии, но трудоемкая в реализации
задача.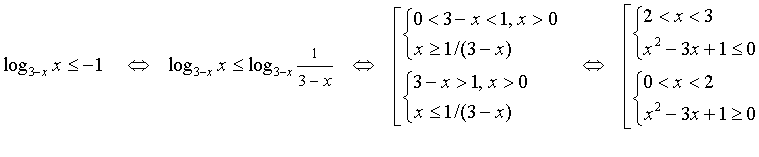
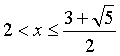 ,
а из второй -
,
а из второй - 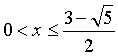 . Таким
образом, получаем ответ:
. Таким
образом, получаем ответ: 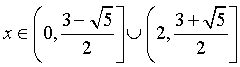 .
.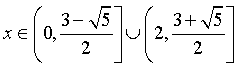 .
.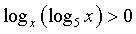 .
.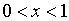 , и
второй, когда
, и
второй, когда 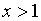 .
.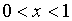 . При
этих значениях
. При
этих значениях 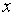 ,
, 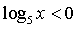 и тогда левая часть не определена. То есть
ни одно значение
и тогда левая часть не определена. То есть
ни одно значение 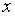 интервала
интервала 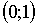 не входит
в решение.
не входит
в решение.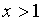 . Наше
неравенство эквивалентно следующему:
. Наше
неравенство эквивалентно следующему: 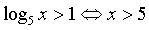 ,
что в совокупности с условием
,
что в совокупности с условием 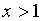 ,
дает промежуток решения
,
дает промежуток решения 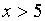 .
.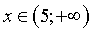 .
.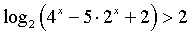 .
.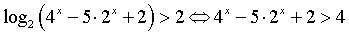 .
Далее заменяем
.
Далее заменяем 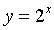 и
приходим к неравенству
и
приходим к неравенству 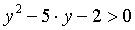 ,
что в совокупности с условием
,
что в совокупности с условием 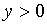 дает
дает 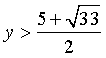 . Делаем
обратную замену:
. Делаем
обратную замену: 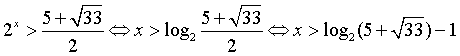 .
.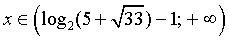 .
.