Пример 2.1.
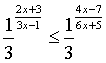 - простой пример, который
продолжает дело предыдущего параграфа. «Показательность»
в этом случае почти формальна.
- простой пример, который
продолжает дело предыдущего параграфа. «Показательность»
в этом случае почти формальна.РЕШЕНИЕ: так как
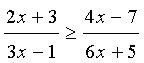 .
Перенесем все в левую часть, приведем к
общему знаменателю:
.
Перенесем все в левую часть, приведем к
общему знаменателю:
Показательные неравенства
Пример
2.1. 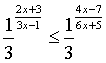 - простой пример, который
продолжает дело предыдущего параграфа. «Показательность»
в этом случае почти формальна.
- простой пример, который
продолжает дело предыдущего параграфа. «Показательность»
в этом случае почти формальна.
РЕШЕНИЕ: так как ![]() ,
то наше неравенство эквивалентно
неравенству
,
то наше неравенство эквивалентно
неравенству 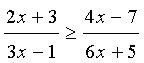 .
Перенесем все в левую часть, приведем к
общему знаменателю:
.
Перенесем все в левую часть, приведем к
общему знаменателю:

ОТВЕТ: 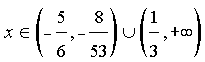 .
.
Пример
2.2. ![]() -
решение просто и без изысков; однако
требуется понять, что нужно сначала сделать
замену
-
решение просто и без изысков; однако
требуется понять, что нужно сначала сделать
замену ![]() ,
получить неравенство вида
,
получить неравенство вида ![]() ,
решить его и потом вернуться к переменной
,
решить его и потом вернуться к переменной ![]() .
.
РЕШЕНИЕ: Сделав замену ![]() и получив неравенство
и получив неравенство ![]() ,
имеем:
,
имеем: ![]() .
Возвращаясь к переменной
.
Возвращаясь к переменной ![]() ,
получим
,
получим ![]() ,
и так как
,
и так как ![]() при любых значениях
при любых значениях ![]() ,
наше неравенство эквивалентно неравенству
,
наше неравенство эквивалентно неравенству ![]() ,
что выполняется при
,
что выполняется при ![]() .
.
ОТВЕТ: ![]() .
.
Пример
2.3.  - задача придумана без
особого контроля качества корней; вновь в
учебных целях метод важнее результата:
здесь на самом деле самым эффективным
является (обобщенный) метод интервалов. Для
тех, кто пожелает свести неравенство с
двумя множителями к совокупности систем (такие
желающие есть практически всегда) можно
добавить еще парочку множителей, которые
сделают данный путь совсем невозможным и
добавят ловушек в эту задачу.
- задача придумана без
особого контроля качества корней; вновь в
учебных целях метод важнее результата:
здесь на самом деле самым эффективным
является (обобщенный) метод интервалов. Для
тех, кто пожелает свести неравенство с
двумя множителями к совокупности систем (такие
желающие есть практически всегда) можно
добавить еще парочку множителей, которые
сделают данный путь совсем невозможным и
добавят ловушек в эту задачу.
РЕШЕНИЕ: Преобразуем второй
множитель в неравенстве 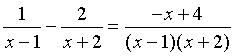 .
Определим точки, в которых обращается в
нуль первый или второй множители и где
второй множитель не определен. Это
.
Определим точки, в которых обращается в
нуль первый или второй множители и где
второй множитель не определен. Это ![]() ,
,
![]() ,
, ![]() .
Рассмотрим следующие промежутки на
числовой оси:
.
Рассмотрим следующие промежутки на
числовой оси: ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
1) ![]() .
На данном промежутке
.
На данном промежутке ![]() и первый множитель положителен. Второй
множитель также положителен, исключая
точку
и первый множитель положителен. Второй
множитель также положителен, исключая
точку ![]() ,
где он не определен. Таким образом,
промежуток
,
где он не определен. Таким образом,
промежуток ![]() входит в решение.
входит в решение.
2) ![]() .
На данном промежутке первый множитель
положителен, а второй отрицателен или не
определен (в точках
.
На данном промежутке первый множитель
положителен, а второй отрицателен или не
определен (в точках ![]() и
и ![]() ).
Точки этого промежутка не входят в решение.
).
Точки этого промежутка не входят в решение.
3) ![]() .
Здесь
.
Здесь ![]() и
первый множитель неположителен. Второй
множитель отрицателен, исключая точку
и
первый множитель неположителен. Второй
множитель отрицателен, исключая точку ![]() ,
где он не определен. Получаем, что
промежуток
,
где он не определен. Получаем, что
промежуток ![]() входит в решение.
входит в решение.
4) ![]() .
Здесь первый множитель положителен, а
второй отрицателен или не определен (в
точке
.
Здесь первый множитель положителен, а
второй отрицателен или не определен (в
точке ![]() ).
Точки этого промежутка не входят в решение.
).
Точки этого промежутка не входят в решение.
5) ![]() .
Точки этого промежутка входят в решение.
.
Точки этого промежутка входят в решение.
Получаем ответ: ![]() .
.
ОТВЕТ: ![]() .
.
Пример
2.4. 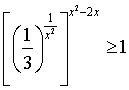 - в данной задаче основная
сложность заключена в правильном
потенцировании неравенства. Однако сразу
видно, что показатели можно перемножить.
После чего задача решается стандартным
подходом.
- в данной задаче основная
сложность заключена в правильном
потенцировании неравенства. Однако сразу
видно, что показатели можно перемножить.
После чего задача решается стандартным
подходом.
РЕШЕНИЕ: Перемножит показатели,
получим  .
В последнем неравенстве знаменатель
неотрицателен при любых значениях
.
В последнем неравенстве знаменатель
неотрицателен при любых значениях ![]() ,
и неравенство эквивалентно совокупности
,
и неравенство эквивалентно совокупности 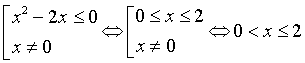 .
.
ОТВЕТ: ![]() .
.
Пример
2.5. ![]() .
.
РЕШЕНИЕ: Преобразуем неравенство
к виду 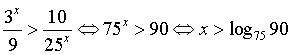 .
.
ОТВЕТ: ![]() .
.