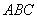 проведены высоты
проведены высоты 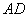 и
и 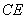 . Найти
. Найти 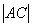 ,
если
,
если 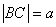 ,
, 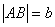 и
и 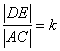 .
.|
Задача 9 из 20 |
В треугольнике
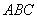 проведены высоты
проведены высоты 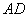 и
и 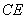 . Найти
. Найти 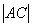 ,
если
,
если 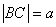 ,
, 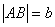 и
и 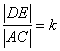 .
.
Решение:
Обозначим 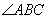 за
за
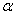 . Тогда в прямоугольном
. Тогда в прямоугольном 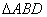 имеем:
имеем: 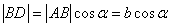 . А в прямоугольном
. А в прямоугольном 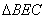 имеем:
имеем: 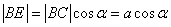 . В
. В 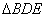 по теореме косинусов
по теореме косинусов 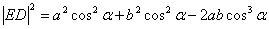 , в
, в 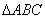 по теореме косинусов
по теореме косинусов 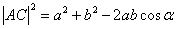 .
.
По условию 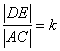 ,
имеем:
,
имеем: 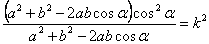 . Отсюда
. Отсюда 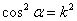 .
.
В случае, если угол 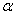 острый,
острый, 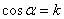 и
и 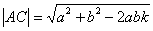 .
.
В случае, если угол 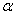 тупой,
тупой, 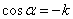 и
и 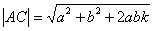 .
.