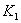 и
и 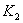 , другая - в точках
, другая - в точках 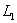 и
и 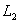 . Доказать, что прямая
. Доказать, что прямая 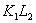 высекает на этих окружностях хорды равной длины.
высекает на этих окружностях хорды равной длины.|
Задача 8 из 20 |
В угол
вписаны две окружности, одна из которых касатется сторон угла в точках 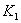 и
и 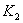 , другая - в точках
, другая - в точках 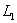 и
и 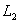 . Доказать, что прямая
. Доказать, что прямая 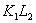 высекает на этих окружностях хорды равной длины.
высекает на этих окружностях хорды равной длины.
Решение:
Пусть 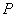 - точка
пересечения прямой
- точка
пересечения прямой 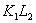 с первой окружностью
(с точками касания
с первой окружностью
(с точками касания 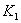 и
и 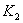 ),
а
),
а 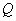 - точка пересечения прямой
- точка пересечения прямой 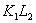 со второй окружностью. Воспользуемся тем, что квадрат касательной равен произведению
отрезков секущей, проведенной из той же точки:
со второй окружностью. Воспользуемся тем, что квадрат касательной равен произведению
отрезков секущей, проведенной из той же точки: 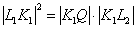 ,
,
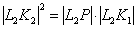 .
.
Так как 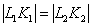 , получим
, получим
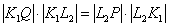 , тогда
, тогда 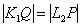 .
.
Прибавив к обеим частям этого равенства 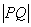 (или отняв от обеих частей
(или отняв от обеих частей 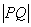 в зависимости
от расположения точек
в зависимости
от расположения точек 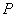 и
и 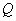 на прямой
на прямой 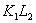 ) получим искомое:
) получим искомое: 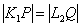 .
.