На диагонали
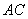 выпуклого четырехугольника
выпуклого четырехугольника  находится центр окружности радиуса
находится центр окружности радиуса 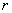 ,
касающейся сторон
,
касающейся сторон  ,
, 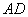 и
и 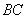 . На диагонали
. На диагонали  находится центр окружности радиуса
находится центр окружности радиуса 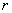 ,
касающейся сторон
,
касающейся сторон 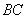 ,
,  и
и 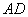 . Найти площадь данного четырехугольника
. Найти площадь данного четырехугольника
 , если известно, что окружности
касаются друг друга внешним образом.
, если известно, что окружности
касаются друг друга внешним образом.
Решение:
Пусть в данном четырехугольнике 
 и
и 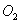 - центры окружностей, лежащие на диагоналях
- центры окружностей, лежащие на диагоналях 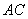 и
и  . Точки
. Точки 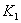 ,
,
 ,
, 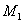 являются точками касания окружности с центром
являются точками касания окружности с центром  со сторонами
со сторонами 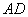 ,
,  и
и 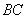 соответственно, точки
соответственно, точки 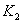 ,
,
 ,
, 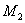 - точки касания окружности с центром
- точки касания окружности с центром 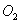 со сторонами
со сторонами 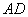 ,
,  ,
,
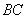 ,
,  - основание высоты, опущенной из
- основание высоты, опущенной из  на
на 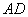 .
.
По условию окружности равны и касаются друг друга, следовательно,
общие касательные параллельны:  .
Далее,
.
Далее, 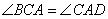 (накрест лежащие). Так
как
(накрест лежащие). Так
как  и
и 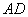 касательные, а
касательные, а 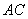 проходит через центр
окружности
проходит через центр
окружности  , то, следовательно,
, то, следовательно,
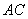 - биссекриса
- биссекриса 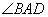 и
и  . Следовательно,
. Следовательно,  ,
откуда
,
откуда 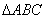 - равнобедренный и
- равнобедренный и 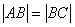 .
Так как
.
Так как  и
и  ,
то
,
то  - либо равнобочная трапеция,
либо параллелограмм. Но параллелограммом
- либо равнобочная трапеция,
либо параллелограмм. Но параллелограммом  быть не может, так как
быть не может, так как  и
и 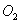 должны лежать на средней линии
должны лежать на средней линии  ,
а в параллелограмме диагонали точкой пересечения делятся пополам, то есть центры
окружностей должны были совпасть, что невозможно по условию.
,
а в параллелограмме диагонали точкой пересечения делятся пополам, то есть центры
окружностей должны были совпасть, что невозможно по условию.
Пусть 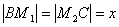 .
Тогда
.
Тогда 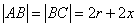 . Но
. Но 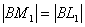 как отрезки касательных, проведенных к окружности из одной точки, тогда
как отрезки касательных, проведенных к окружности из одной точки, тогда 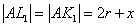 .
По построению
.
По построению 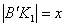 , следовательно,
, следовательно,  ,
,
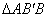 равнобедренный и прямоугольный,
то есть
равнобедренный и прямоугольный,
то есть 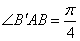 . Соответственно,
. Соответственно, 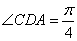 ,
,
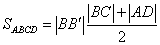 , где
, где 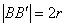 ,
,
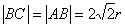 ,
, 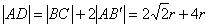 .
.
Ответ:  .
.
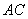 выпуклого четырехугольника
выпуклого четырехугольника  находится центр окружности радиуса
находится центр окружности радиуса 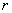 ,
касающейся сторон
,
касающейся сторон  ,
, 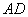 и
и 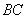 . На диагонали
. На диагонали  находится центр окружности радиуса
находится центр окружности радиуса 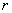 ,
касающейся сторон
,
касающейся сторон 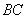 ,
,  и
и 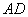 . Найти площадь данного четырехугольника
. Найти площадь данного четырехугольника
 , если известно, что окружности
касаются друг друга внешним образом.
, если известно, что окружности
касаются друг друга внешним образом. и
и 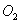 - центры окружностей, лежащие на диагоналях
- центры окружностей, лежащие на диагоналях 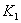 ,
,
 ,
, 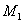 являются точками касания окружности с центром
являются точками касания окружности с центром 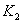 ,
,
 ,
, 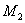 - точки касания окружности с центром
- точки касания окружности с центром  - основание высоты, опущенной из
- основание высоты, опущенной из  на
на  .
Далее,
.
Далее, 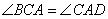 (накрест лежащие). Так
как
(накрест лежащие). Так
как 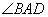 и
и  . Следовательно,
. Следовательно,  ,
откуда
,
откуда 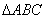 - равнобедренный и
- равнобедренный и 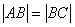 .
Так как
.
Так как  ,
то
,
то 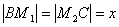 .
Тогда
.
Тогда 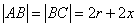 . Но
. Но 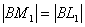 как отрезки касательных, проведенных к окружности из одной точки, тогда
как отрезки касательных, проведенных к окружности из одной точки, тогда 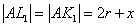 .
По построению
.
По построению 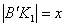 , следовательно,
, следовательно,  ,
,
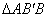 равнобедренный и прямоугольный,
то есть
равнобедренный и прямоугольный,
то есть 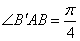 . Соответственно,
. Соответственно, 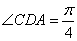 ,
,
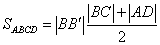 , где
, где 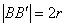 ,
,
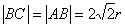 ,
, 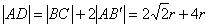 .
. .
.