Центры двух окружностей с радиусами и лежат на гипотенузе прямоугольного треугольника. Одна окружность касается двух катетов, другая катета и первой окружности. Найти стороны треугольника.

Решение:
    Пусть - данный треугольник, угол - прямой, и - центры окружностей с радиусами и , и - точки касаний окружностями катета . Проведем параллельно и обозначим через . Тогда из имеем: .
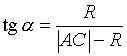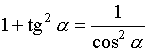    Отметим, что , следовательно и из имеем: . Используя тождество , получим: .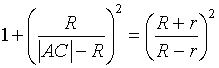
    Отсюда 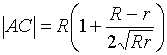; ; .
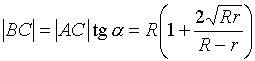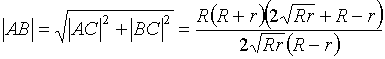