 проходят через одну точку, то три другие точки попарного пересечения этих окружностей
лежат на окружности радиуса
проходят через одну точку, то три другие точки попарного пересечения этих окружностей
лежат на окружности радиуса  .
.|
Задача 15 из 20 |
Доказать,
что если три окружности радиуса  проходят через одну точку, то три другие точки попарного пересечения этих окружностей
лежат на окружности радиуса
проходят через одну точку, то три другие точки попарного пересечения этих окружностей
лежат на окружности радиуса  .
.
Решение:
Пусть все три окружности радиуса  с центрами
с центрами 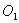 ,
, 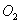 и
и 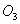 пересекаются в точке
пересекаются в точке 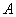 и попарно пересекаются в точках
и попарно пересекаются в точках 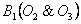 ,
,
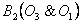 ,
, 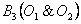 .
Очевидно, что середины
.
Очевидно, что середины 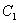 ,
, 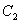 и
и 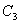 отрезков
отрезков 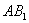 ,
,
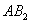 и
и 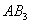 являются в то же время серединами отрезков
являются в то же время серединами отрезков 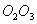 ,
,
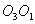 и
и 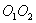 (общая хорда пересекается с отрезком, соединяющим центры окружностей). Поэтому
у каждого из треугольников
(общая хорда пересекается с отрезком, соединяющим центры окружностей). Поэтому
у каждого из треугольников 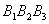 и
и 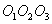 стороны соответственно вдвое больше сторон треугольника
стороны соответственно вдвое больше сторон треугольника 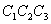 и параллельны им. Следовательно,
и параллельны им. Следовательно, 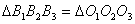 .
Но радиус описанной около
.
Но радиус описанной около 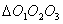 окружности
равен, очевидно,
окружности
равен, очевидно,  (
(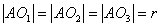 ).
Следовательно, радиус описанной около
).
Следовательно, радиус описанной около 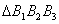 окружности равен
окружности равен  .
.