С.Г. Шеховцов
Эвристика Евклида:
экзотерическое и эзотерическое
в античном образовании
ОГЛАВЛЕНИЕ
Неожиданный
Евклид: от теоремы Пифагора к ножницам..
Проблемы,
задачи, решения и оформление результатов
Заключение.
Немного о контекстной обработке информации
Введение. Постановка задачи
Как известно, самое надёжное знание то, что выстроено самостоятельно. Насколько трудно достичь такой обретённости знания в обучении также хорошо известно, особенно если речь идёт об обучении современному научному знанию. Ведь чем совершеннее формы такого знания, тем глубже в них скрыты априорные мысленные модели, которыми было вызвано их построение.
Нет ничего более важного, чем умение найти источник открытия – это, по-моему, ещё интереснее, чем сделать само открытие.
Г.В. Лейбниц
Отец технологичных форм научного знания, изобретший способ обучения пользоваться анализом (и преподавать его) людей вовсе его не понимающих, намеревался написать сочинение «Искусство изобретения», но… не успел, остались лишь отдельные фрагменты.
Эта информация из рецензии на знаменитую книгу G. Polya “How to solve it” [Гайдук Ю.М] звучит вполне правдоподобно. В рецензии также говорится, что задолго до Лейбница изучением «способов делать открытия и изобретения», т. е. эвристикой, занимался автор “Начал” Евклид, и что сообщает это Папп Александрийский. А это уже удивительно! Главный и самый знаменитый труд Евклида известен совсем иным.
…с той же эпической медленностью движется изложение через все 470 предложений эвклидовых “Элементов”. Каждое из них защищено процессом доказательства, с соблюдением одинаковых логических формальностей, невольно вызывающих на сравнение с юридическими обрядами судебной защиты; великий адвокат геометрической истины каждый раз предусматривает все мельчайшие возражения “противоположной стороны”, для которой опущение хотя бы самого очевидного силлогизма, хотя бы одной логической формальности даст повод к кассации всего доказательства; сходство простирается до привидения налицо всех свидетелей защиты в виде дословного цитирования раньше доказанных теорем, подтверждающих её положения[1]. Стараясь не убедить, а победить читателя, в котором Эвклид как бы видит опытного диспутанта-софиста, автор мало заботится об удобствах понимания истины, подчас загораживая её непомерно длинным рядом аргументов.
Никаких разъяснений не дано, чтобы облегчить понимание чисто формальных определений, рядом которых начинается каждая книга; они приведены не для выяснения содержания понятий во всём их объёме, а лишь как исходные пункты диалектического состязания, условно принятые обеими сторонами[2].
Наконец за немногими исключениями, Эвклид нигде не посвящает читателя в тот анализ, которым добыто доказательство; оно всегда излагается догматически в законченной синтетической форме и нередко производит на “противоположную сторону” впечатление искусно построенной, но неожиданной аргументации речи адвоката.
[ Шереметевский
В.П., с. 138-139]
Процитированный историко-математический очерк известного до революции математика-педагога В.П. Шереметевского был написан с целью обогащения хорошей, но суховато-прагматичной книги Г. Лоренца «Элементы высшей математики», которая была некогда выбрана Комиссией по организации домашнего чтения для «Библиотеки для самообразования». В этом очерке есть также высказывание одного из самых ранних и самых выдающихся просветителей средневековья Роджера Бэкона:
Только розгами можно вогнать ученикам четыре первых теоремы эвклидовых «Элементов», а пятая[3] уже называется elefuga – бегство несчастного!
Плохим виделось Р. Бэкону современное ему преподавание математики. Видеть это было ему больно, ввиду понимания важности математики для человека, а не для специалиста. Ведь, согласно Р. Бэкону, она «одна может очистить разум и сделать учащегося способным к восприятию знания»; «будучи самой лёгкой, она представляет введение к более трудным наукам»; «в ней вещи, известные нам, тождественны с вещами, известными природе»; она – и «дверь и ключ к науке»[4].
В ХХ веке, как известно, стал преобладать иной взгляд на математику и, в частности, на геометрию.
Сегодня, кажется, уже почти все согласны с тем, что традиционная система Евклида, в русской литературе наиболее последовательно проведённая в созданных ещё в прошлом веке учебниках Киселёва [Киселёв А.], не заслуживает сохранения: ведь ни в науке, ни в практической жизни выпускнику средней школы далее не придётся иметь дело с многими теоремами сложившегося курса геометрии и с типичными для этого курса методами рассуждений.
Из предисловия И.М. Яглома к [Шоке Э.]
Согласие, что изучать математику нужно ради её применения в науке или – более общо – в практической жизни, неизбежно меняет её характер ввиду утраты общекультурного смысла. Математика превращается в разнообразные формы математических знаний. Если жизнь, к примеру, филолога, не требует применения таких форм знания, то незачем их и изучать, тем более, что не хватает времени на другие, «нужные» для профессиональной жизни предметы.
Позиция Р. Бэкона заметно иная: «математика есть азбука натуральной философии», т. е. начало понимания природы. Другое дело – годятся ли «Элементы» Евклида в качестве инструмента обучения этой «азбуке».
Изложение должно быть наглядным; последнее невозможно без опыта; у нас в руках есть три средства познавания: авторитет, мышление и опыт. Авторитет не имеет значения, если справедливость его не может быть доказана: он не учит, он требует только согласия. При мышлении мы обыкновенно отличаем истинный аргумент от ложного, проверяя вывод опытом. Экспериментальная наука испытывает и проверяет выводы других наук, она исследует тайны природы собственными силами.
[Шереметевский В.П.,
с. 233]
Образовательную сторону «Элементов» находил неудовлетворительной не один Роджер Бэкон.
И для случая неравных катетов, как и вообще для всякой геометрической истины, должно существовать подобное наглядное доказательство – хотя бы потому, что открытие истины всегда имело в своей основе созерцаемую необходимость, а доказательство придумывалось только потом.
А. Шопенгауэр [Литцман В., c. 38-39]
Налицо противоречие. Евклид занимался в своей школе
эвристикой – не доверять Паппу нет оснований. В книгах «Элементов» следов
эвристики не видно – по крайней мере, их не сумели разглядеть совсем не
равнодушные к ценности этого сочинения люди. Вывод, вмещающий оба эти аспекта,
сделать несложно. Евклид, очевидно, сделал то, что хотел. Назначение
эвристики – делать умнее учеников, а не демонстрировать ум и достижения учёного
и преподавателя тем, кто способен это оценить, разумеется. Ученикам мало что
даёт демонстрация построенной единой
конструкции языка и системы высказываний, истинность которых вытекает из
истинности других высказываний (доказанных прежде или изначально принятых без
доказательства); её цель, очевидно, иная – явно предъявить тем, кто уже
понимает смысл этой организационной
задачи, вариант такой организации на материале математики. Судя по всему, это
удалось: «Элементы» долго были недостижимым эталоном научности. В рамках
решения такой задачи «ходульная» демонстрация истинности теоремы Пифагора
выполнена Евклидом весьма оптимально.
… для доказательства… нужно провести всего три вспомогательных линии … Теоремы нам потребуются лишь следующие: один раз первый признак равенства треугольников и дважды – теорема о том, что если параллелограмм и треугольник имеют одинаковые основание и высоту, то площадь параллелограмма равна удвоенной площади треугольника.
Теперь нам ясно, что если доказательство Евклида рассматривать в рамках всей построенной в «Началах» системы, то его нужно признать чрезвычайно простым.
[Литцман В.,
c. 41]
Эта простота особого рода – так сказать, простота формы регистрации итога. «Наглядность» же, о которой говорят и наличие которой считают необходимой Р. Бэкон и А. Шопенгауэр, должна быть потенциально способна открывать путь построения своего доказательства, т. е. должна явно указывать на некий, доступный каждому операциональный и организационный опыт, способствующий достижению результата. Кто-то увидит эти указания, кто-то нет, но первое самостоятельно выстроенное доказательство может оказаться весьма громоздким по исполнению, зато его всегда будет овевать простота видения, его вызвавшего. Другая это простота… простота «созерцаемой необходимости». То, что Евклид культивировал её, но не представил в «Элементах» перекликается с другим античным сюжетом.
Александр, по-видимому, не только усвоил учения о нравственности и государстве, но приобщился и к тайным более глубоким учениям, которые философы называли "устными" или "скрытыми" и не предавали широкой огласке. Находясь уже в Азии, Александр узнал, что Аристотель некоторые из этих учений обнародовал в книгах, и написал ему откровенное письмо в защиту философии, текст которого гласит: "Александр Аристотелю желает благополучия! Ты поступил неправильно, обнародовав учения, предназначенные только для устного преподавания. Чем же мы будем отличаться от остальных людей, если те самые учения, на которых мы были воспитаны, сделаются общим достоянием? Я хотел бы превосходить других не столько могуществом, сколько знаниями о высших предметах. Будь здоров".
Плутарх. Александр, 7
Ответ Аристотеля гласил:
[Лосев А.Ф.,
Тахо-Годи А.А., c.
272-273]
Придание результатам мысленного моделирования систематической и регистрационно-простой формы не означает оглашения смыслов. Смыслы вообще нельзя передать; всякий раз каждый человек открывает их для себя заново. Передаются и воспроизводятся только формы деятельности и организации знания. Чем они совершеннее, тем больше они оторваны от первородных смыслов. Эти-то смыслы и оказываются, в итоге, «тайными».
Этот эффект можно назвать «Утратой Творца». Услышать голос Творца в итоговых формах научного знания не просто. Вообще, эта задача изоморфна Богоискательству, и потому она не всякому по плечу. Аристотель, разумеется, это прекрасно понимал, и пытался донести это до своего ученика.
Но настали времена эффективных форм – времена операционально-доступных многим научных форм деятельности и организации знания. Сегодня академическое издание предлагает к приведённому фрагменту жизнеописания Александра примечание:
Среди сочинений Аристотеля, действительно, были "эксотерические", предназначенные для всякого читателя, и "эсотерические", предназначенные для учеников и последователей, но "таинственность" их Плутархом преувеличена.
[Плутарх, с.
584]
Написано оно М.Л. Гаспаровым – филологом-классиком, ныне академиком РАН. В самом деле, ну какие могут быть тайны в античных научных сочинениях для современного учёного, выросшего в условиях бурного научно-технического прогресса! Ведь наука и техника, как известно, ушли далеко вперёд, и, значит, современный учёный знает больше и лучше своих античных коллег. Это современный математик не видит, на чём основывался эвристический опыт Евклида. У филолога, естественно, такой проблемы нет – не его это специальность, поэтому ему и так всё ясно.
Возникает вопрос: можно ли, опираясь на текст Евклида, реконструировать его эвристическую практику – найти тот источник открытия, о котором говорил Лейбниц?
Ситуация любопытная. Ведь если удастся обнаружить следы эвристики Евклида и выйти на её истоки, то: некоторые конкретные черты приобретут и слова про «устные» или «скрытые» учения, и про их таинственность, и про «утрату творца»; возникнет возможность увидеть, может ли эвристический опыт Евклида оказаться ценным сегодня, т. е. для будущего образования. Окажись это хоть в чём-то так, возникнет вопрос, что, собственно, было возрождено в Эпоху Возрождения, а что ещё только предстоит возродить и – главное – почему это не удалось прежде?
Уточним задачу. Требуется, исходя из содержания «Элементов», найти элементарную в смысле доступности всем деятельностную операцию, следствием использования которой оказались бы представленные Евклидом результаты?
Неожиданный Евклид: от теоремы Пифагора к ножницам
Итак, Евклидово доказательство теоремы Пифагора, метко названное Шопенгауэром «ходульным», никто не считает наглядным. Можно ли, исходя из него, установить ход его построения и выделить операцию, на которой оно основано? Оказывается можно и даже совсем нетрудно.
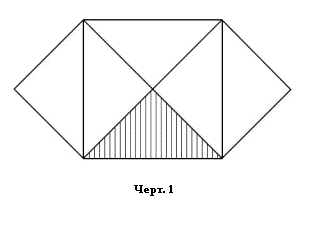
Доказательство Евклидом Предложения 47 [НАЧАЛА, сс. 58-59]
основано на следующей цепочке равенств треугольников:
BFH = BFC = BAD = BLD.
«Равны не треугольники, а их площади! Это знают все… со школы». Могут так сказать, и будут правы. Сегодня равенство фигур понимают существенно ýже, а теорему Пифагора формулируют на языке площадей. Нетрудно, разумеется, написать, как это принято сегодня:
SBFH = SBFC = SBAD = SBLD .
Но… это предполагает предварительное введение числовой функции (величины)
S: фигура ® Sфигура ,
определённой, по крайней мере, для фигур, участвующих в построениях. Но у Евклида не так!
В Первой книге у Евклида нет величин, а есть – отношение равенства!
Сравнивать, уравнивать, выравнивать… – это всё синонимы; операциям с такими именами «равенство» должно, очевидно, предшествовать. Так что, у Евклида всё естественно, и всё на своих местах. Это-то и оказалось неожиданным[5].
Итак, Книга первая, Предложение 47 [НАЧАЛА, с. 58]:
В прямоугольных треугольниках квадрат на стороне, стягивающей прямой угол, равен < вместе взятым > квадратам на сторонах, заключающих прямой угол.
В угловых скобках переводчик, Д.Д. Мордухай-Болтовской помещал добавления, «необходимые для понимания иногда слишком сжатого текста Евклида». Слова «…вместе взятым…» не потребовались бы, если бы в формулировке фигурировали числа; все знают, их можно складывать, образуя этим другие числа – суммы. Стало быть, кроме отношения «равенства» в предложении есть операция «взятия вместе», «составления» или «сложения» квадратов. Составить два произвольных квадрата вместе можно, разумеется, по всякому, но как сложить их в квадрат?
Теорема Пифагора в форме Евклида даёт простой алгоритм сложения квадратов, равно как и вычитания из большего квадрата меньшего: квадрат на гипотенузе – сумма, каждый из квадратов катетов – соответствующая разность.
Неслучайно, разумеется, в учебнике элементарной геометрии А. Киселёва [Киселёв А., сс. 246-249] сразу вслед за теоремой Пифагора (п. 321), данной на языке размеров площадей, приводятся именно задачи на построение «суммы» и «разности» квадратов, а также задача построения квадрата, площадь которого находится в заданном отношении к площади данного квадрата (п. 322). Зачем там приводятся эти задачи, не вполне понятно; выглядят они как применения теоремы Пифагора вот к таким задачам на построение.
Зачем нужны эти построения? Вспомним приведённое выше высказывание И.М. Яглома. Если не дать внятного ответа на этот вопрос, с ним, пожалуй, можно согласиться – зачем, в самом деле, нужно учить решения этих «чертёжных» задач, где и когда они могут потребоваться «по жизни»!?
Эта неясность возникает не из-за следования А. Киселёвым «системе Евклида», как это кажется И.М. Яглому, а из-за её нарушения, случившегося задолго до А. Киселёва.
«Она предшествует другим наукам о природе, ибо изучает количество, которое воспринимается интуитивно». Написал это о математике Роджер Бэкон в середине 13-го века (см. сноску 4). К этому высказыванию В.П. Шереметевский в скобках добавляет: «intuitu intellectus; Бэкон считал основные истины математики врождёнными, т. е. независимыми от опытного знания». В поле такого взгляда математика предстаёт как инструмент количественного описания мира.
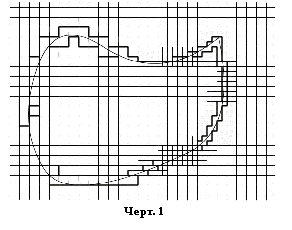В системе Евклида неясности нет.
Предложение 47, предоставляя возможность заменить любую конечную
совокупность квадратов одним им равным, сводит задачу сравнения самых разных
фигур к сравнению квадратов (см. Черт. 4). Сравнение квадратов, как
видно уже не из самого Предложения, а из его доказательства Евклидом, легко
сводится к сравнению отрезков, на которые разбивает гипотенузу опущенный из
прямого угла перпендикуляр. Возникает численное отношение, в котором любой
возможный квадрат находится с квадратом, выбранным в качестве эталона.
Таким образом, теорема Пифагора оказывается важным звеном в цепочке организации измерения, именно как процедура сложения квадратов. Но в этом качестве она оказывается ненужной, если понятие величины площади введено априори – из «врождённой интуиции». Система распадается.
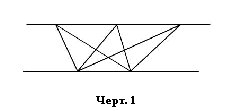Чтобы понять, в чём процедурно заключается
сложение двух квадратов в квадрат, вернёмся к доказательству Евклидом теоремы
Пифагора. Для его построения он пользуется описанными ранее (Предложения 37-40)
классами равных треугольников. Это – треугольники, заключённые между двух
параллельных. На одной из них располагаются их основания, на другой – вершины. Если равны основания, равны и треугольники
(Черт. 5). Это означает, что все треугольники, получающиеся изменением
положения вершины на «верхнем рельсе», равны между собой. То же, разумеется,
будет верно при изменении положения основания на «нижнем рельсе».
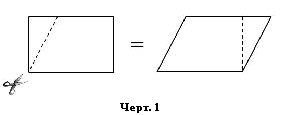Это
обстоятельство – прямое следствие наличия классов равных параллелограммов,
которые Евклид вводит в Предложениях 35-36. Параллелограммы, заключённые между двух параллельных
прямых, основания которых равны, равны между собой. Этот
результат становится совершенно прозрачным, если выполнить очень простую
операцию реорганизации такого участка (Черт. 6). При повторении снова и
снова этой операции параллелограммы будут становиться всё более и более
«вытянутыми». «Тесто» же, из
которого слеплен каждый из них, не привносится и не удаляется. Это
обстоятельство и фиксируется отношением равенства,
которым пользуется Евклид. В сущности, его равенство
– своеобразный принцип сохранения
пространства.
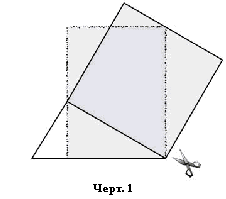Несмотря на
доступность, в книгах «Элементов» эта операция явно не представлена; для
доказательств (демонстраций истинности) она неудобна: их лучше строить сразу
для общего случая, исходя из уже выстроенной, итоговой картины. Однако она
очень полезна в эвристических целях. Возникающие с её участием задачи на
сообразительность столь просты, что доступны в детском саду. Обретаемый таким
образом опыт игры в реорганизацию формирует навык иного, можно сказать,
«подвижного» видения. К примеру, совсем нетрудно догадаться, как квадрат на катете (Черт. 7) в «два хода»
превратить в прямоугольник, опирающийся на гипотенузу. Изучение переставляемых
кусочков легко позволит узнать в нём часть квадрата гипотенузы,
пропорциональную занятой на ней части. Превращение квадрата с соседнего катета
в прямоугольник, опирающийся на соседнюю часть гипотенузы, потребует несколько
большей работы ножницами. Помимо полезного опыта это даст также стимул к
переходу от «резания» к «вычерчиванию» итога. На таком пути неизбежно обретение
«подвижного» видения; линии предстанут как образующие «тождественных», не
добавляющих пространства преобразований параллелограммов и треугольников.
Наличие такого опыта уже не позволит стереть в сознании базовую операцию, которая сделала легко доступным обретение столь обогащённого зрения. Её состав – отнимание, прибавление и равенство – должен, следовательно, играть фундаментальную роль в Евклидовой картине математики. Все эти элементы операции реорганизации мы и обнаруживаем в самом начале Евклидовых книг в разделе ОБЩИЕ ПОНЯТИЯ или Аксиомы:
1. Равные одному и тому же равны между собой.
2. И если к равным прибавляются равные, то и целые будут равны.
3. И если от равных отнимаются равные, то остатки будут равны.
4. И если к неравным прибавляются равные, то целые будут не равны.
5. И удвоенные одного и того же равны между собой.
6. И половины одного и того же равны между собой.
7. И совмещающиеся друг с другом равны между собой.
8. И целое больше части.
9. И две прямые не содержат пространства.
[НАЧАЛА, с. 15]
Ясно, что выделение состава операции и формулировка свойств его элементов – задача посильная очень многим, по существу, всем, если исходить из опыта обращения с нею. Без такого опыта Аксиома 9, например, может показаться странной, и её интерпретация может вызывать затруднения. В контексте же операции её смысл прост и ясен всякому: пары границ, возникающие при отнимании и исчезающие при прибавлении, пространства не имеют, ибо его не привносят и не удаляют сами эти операции. Это свойство характеризует выбор мысленной модели, ведь в материальном мире можно представить множество ситуаций, когда это не так[6]. Стало быть, её истинность следует принять без доказательства в качестве характерного свойства соответствующего мира мысленных моделей.
В итоговой форме заметить присутствие столь простой операции мешает восприятие текста «Элементов» как материала для выучивания и применения, в особенности, когда учебный процесс модернизирован под первенство количества и величины как intuitu intellectus. Судя по всему, Евклид не считал, подобно Роджеру Бэкону, «математические истины» присущими человеку от природы, а видел в них последствия организационного опыта – так сказать, результат самой способности человека выполнять соответствующие операции по внесению и переустройству порядка. Поэтому величина у него – операция, операция сравнения, а строит он – теорию измерений. Если припомнить шок, испытанный физиками в ХХ веке, когда выяснилось, что физические величины суть операции[7], то математика Евклида становится современнее и много привлекательнее суррогатов, применяемых сегодня в образовании.
Итак, наглядная и доступная операция, позволяющая воображению каждого деятельно включиться в фундаментальное моделирование процесса измерения пространства, у Евклида присутствует, но в скрытом, расчленённом виде. Нет сомнения в том, что она использовалась в школе Евклида в процессе обучения, ведь результаты, представленные в «Элементах», оказываются решениями, в общем-то, нетрудных при наличии такого видения задач. Но практика эта оказалась, в итоге, эзотерической; экзотерическим же (внешним) её проявлением стали «Элементы» Евклида, выполненные как систематически организованная сводка результатов такого моделирования.
Проблемы, задачи, решения и оформление результатов
В связи с навыком видения равенства того, что выглядит неравным, следует всегда иметь в виду, что оно может и не возникнуть; «предложения» же можно запоминать и использовать, даже не видя их простоты и не понимая поэтому, с чего это они истинны. Достаточно, что их истинность доказана… «наукой». Именно по этому поводу Платон высказался в письме родственникам и друзьям Диона.
У меня самого по этим вопросам нет никакой записи и
никогда не будет. Это не может быть выражено в
словах, как остальные науки; только если кто
постоянно занимается этим делом и
слил с ним всю свою жизнь, у него внезапно, как свет, засиявший от искры огня, возникает в душе это
сознание и само себя там питает. И
вот что еще я знаю: написанное и
сказанное мною было бы сказано наилучшим образом, но я знаю также, что написанное плохо причинило бы мне сильнейшее огорчение. Если бы мне
показалось, что следует написать или
сказать это в понятной для многих форме, что более прекрасного могло
быть сделано в моей жизни, чем принести столь великую пользу людям, раскрыв
всем в письменном виде сущность вещей? Но я думаю, что подобная попытка не явилась бы благом для людей, исключая очень
немногих, которые и сами при малейшем
указании способны все это найти; что же касается остальных, то одних это совсем неуместно преисполнило бы несправедливым презрением, а других — высокой, но пустой надеждой, что они научились чему-то
важному.
[Платон. Письмо VII]
Из такой «малости», как операция реорганизации, потенциально многие способны обрести «видение равного» и через это выстроить всё, что необходимо для сравнения – измерения «геометрического блага», т. е. пространства. Мир точек, линий, фигур и тел прост и определёнен. Но не все к этому расположены внутренне. Рассказывают, что один ученик спросил Евклида, какую выгоду может принести ему изучение геометрии, Евклид на это приказал рабу дать ученику обол и добавил: «он хочет извлечь пользу из геометрии». Евклиду же приписывается известный афоризм об отсутствии «царского» пути в науке. Немногими, увы, движет внутренняя радость от обретения видения и понимания, таким людям лишние объяснения только мешают – они лишают их удовольствия самостоятельного открытия. Но без опыта такого простенького, доступного практически каждому открытия и связанного с ним мысленного моделирования трудно рассчитывать на успех в решении задач на «измерение блага» в сложном и неоднозначном мире «полиса»: «Негеометр да не войдёт!»
Что же можно открыть из «тождественных» деформаций фигур?
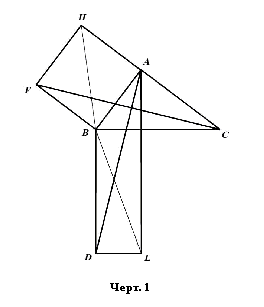
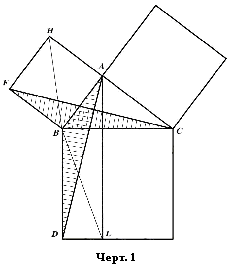Становится ясной
идея доказательства Евклидом теоремы Пифагора. Он просто «переливает»
пространство половинок квадратов катетов в квадрат гипотенузы, заполняя при
этом ровно его половину. Делается это так. Имеющиеся по построению «пути
сообщения» позволяют привести пространство половины катета в касание с
квадратом гипотенузы. Для этого вершина треугольника, содержащего половину
пространства квадрата, перемещается из H в C.
Соответствующее пространство перетекает в треугольник BFC. Это
фиксируется на чертеже. Поворот треугольника на прямой угол по часовой стрелке
пространства не прибавляет и не убавляет; он просто размещает его в другом
треугольнике BAD. Это тоже фиксируется на
чертеже. Получаются «ходули» или «Пифагоровы штаны». Устройство последнего
треугольника позволяет переправить ограниченное им пространство в квадрат
гипотенузы. Это совершается сдвигом его вершины параллельно стороне BD. Из точки A её
можно сместить в любую из двух точек на границе квадрата гипотенузы, например L. Так в итоговом чертеже появляется «рельс» AL, который – по случаю – оказывается перпендикуляром,
опущенным из прямого угла треугольника на его гипотенузу. Перпендикулярность обязана своим появлением квадратам; признаком
же, определяющим движение, является не она, а параллельность стороне квадрата гипотенузы.
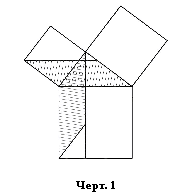Итак,
маршрут перемещения пространства из половины квадрата BFHA в
половину части квадрата гипотенузы проложен. Аналогично прокладывается маршрут
перенесения пространства из половины квадрата другого катета в половину
соседней части квадрата гипотенузы.
Ясно, что такая модель преобразования пространства квадратов принята ради элегантности итоговой картины. Всё то же самое можно проделать и с самими квадратами, правда, «ходули» (это по Шопенгауэру) или «штанишки» (в русской традиции) получатся иного фасона – чуть более мешковатыми (Черт. 9).
Возможен, разумеется, и обратный процесс – разложения квадрата гипотенузы, но для этого нужно сообразить, почему рассечь квадрат следует именно по прямой, проходящей через вершину данного прямоугольного треугольника. Это – если исходить из данности прямоугольного треугольника.
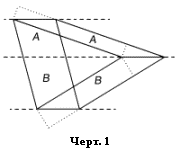Любопытно, что
задача разложения произвольного параллелограмма на параллелограммы же в сумме,
дающие исходный, решается немедленно как простое «удвоение» чертежа для
утверждения равенства параллелограммов, опирающихся основаниями на две
параллельные прямые (Предложение 35 Евклида), которое следует из базовой
операции, представленной Черт. 6. Нужно просто вместо двух
параллельных прямых рассмотреть три (Черт. 10). Исходный параллелограмм
как бы растянут вдоль любой рассекающей его прямой, параллельной основаниям, мы
словно натянули своеобразную тетиву. Пространства A и B частей, на которые разделён исходный параллелограмм,
перекочёвывает в «вытянутые» части. Теперь оно может занимать любой
параллелограмм, зажатый между параллельными прямыми, на которые опираются их
боковые стороны. В частности, пунктиром обозначены прямоугольники, содержащие
те же пространства A и B. Таким образом,
разделение одного параллелограмма на два, которые вместе содержат то же
пространство,
C = A + B,
всегда связано с треугольником, сторонами которого являются основания параллелограммов, вмещающих пространства, участвующие в этом равенстве.
Можно, следовательно, взять любой треугольник, построить на двух его сторонах произвольные параллелограммы и сложить из них параллелограмм на третьей стороне, которая при этом разделится на два отрезка. Их отношение друг к другу естественно принять за отношение, в котором состоят, пространства слагаемых параллелограммов. Этот результат впервые встречается у Паппа Александрийского, причём как «интересное обобщение теоремы Пифагора». Называют его теперь теоремой Паппа, поскольку у Евклида он явно не сформулирован.
Вряд ли, однако, можно сомневаться в том, что человек, придумавший «ходульное» перемещение пространств половинок «катетных» квадратов в половину квадрата гипотенузы, не видел этого простого следствия из своего Предложения, на котором базировалась вся остальная конструкция. Ясно другое. Чертёж 10 даёт общую конструкцию процедур сложения и разложения параллелограммов. Если складываются квадраты, то квадрат в результате возникает только тогда, когда стороны квадратов в точке «составления» образуют прямые, а не ломаные линии.
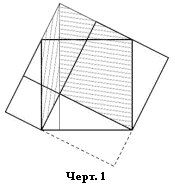В школе Евклида,
без сомнения, было известно много разных форм тождественного перераспределения
пространства. Так, «детское» превращение квадратов катетов в части квадрата
гипотенузы с помощью ножниц (Черт. 7) приводит к Чертежу 11, который
изоморфен Чертежу 10. Кроме того, он является тем, во что превращается
Чертёж 1 в случае неравных катетов с той лишь разницей, что выполнение
сложения квадратов (заштрихованные параллелограммы) приводит к возникновению
«созерцаемой необходимости», легко приводящей к разным способам доказательства.
Так, если его сделать чертёж симметричным (пунктир), то он разделяется на две
знаменитые картинки, которые принято считать «индийским доказательством»
теоремы Пифагора (Черт. 12); правая «разбивка» квадрата получается из левой
соответствующим перемещением прямоугольных треугольников. Правда, на взгляд
автора, несимметричная пара, которая получается сразу, без пунктирного
добавления, ничуть не хуже «индийской».
Черт. 12
Заключение. Немного о контекстной обработке информации
В основе «созерцательной необходимости», о которой говорил Шопенгауэр, лежит счёт одинаковых кусочков. Такое обозрение требует составленности из одинаковых элементов; сравнение пространств, заключённых в фигурах, сводится к сравнению их составов. Примитивная реорганизация пространства приводит к другому «зрению» и, соответственно, к другой «созерцательной необходимости». Равным становится выглядящее неравным, точнее – неодинаковым, и это видение равенства открывает путь к сравнению содержимого самых разных форм с содержимым форм эталонных. Складывается априорная мысленная конструкция (модель) процесса измерения пространства. «Складывается» – это значит, что она может быть сложена самостоятельно, в принципе, каждым. Информацию, благодаря которой становится возможным обретения такого видения предмета, можно называть эвристической. Ведь увидеть что-то для себя новое, значит открыть это.
Но ни модель измерения, ни примитивный организационный опыт, лежащий в её основе, не представлены в книгах Евклида. Их явного описания нет. Демонстрация истинности итоговых форм знания этого не требует. Выявление и обнаружение их скрытого присутствия требует анализа контекста системной организации итоговых форм знания. Другими словами, это – результат контекстного анализа конкретной информации. Такой анализ, вероятно, можно было бы назвать смысловым, но для автора это – синонимы. Настоящая работа, отчасти, иллюстрирует понимание автором слов «контекстная обработка информации».
Информацией является и стройно-последовательное, «медлительное» изложение Евклида, и любые формы визуально-деятельностного представления простейших операций с простейшими фигурами, а также связанные с этими операциями вопросы и выводы, возникающие в связи с этими вопросами. Ясно, что между этими типами информации имеется принципиальное различие. О нём-то и говорится в письме Аристотеля Александру. Разглядеть в стройности итоговых форм простоту и доступность первичного организационного опыта, значит увидеть творца, выстроив итоговые формы заново. Это не очень-то просто. Другое дело, если услышать от творца те «малейшие указания» на такой первичный опыт, которые позволят всё остальное увидеть и сформулировать самостоятельно, быть может, получая попутно какие-то другие «малейшие указания». Это делает необходимым диалог с учителем и ненужным чтение изложения им предмета. Такие «малейшие указания» есть всегда, в любых итоговых формах научного знания! В этом, как, впрочем, и во всём вообще, можно усомниться. Поэтому это утверждение имеет статус ПРИНЦИПА ПОЗНАВАЕМОСТИ.
Исходя из этого принципа, возникновению любых научных форм деятельности и организации знания предшествует априорное мысленное моделирование соответствующих явлений. Оно начинается с опознания сходства с чем-то знакомым и доступным в проявлениях, с каким-то организационным опытом. Принять «отношение сходства» (можно также сказать «равенства» или «эквивалентности») значит заменить реальность моделью. Отождествление модельного организационного опыта с проявлениями бытия рождает язык. Найти эвристические корни научного предмета, значит найти эти внешние подсказки, выявить соответствующий первичный опыт. Сделать его доступным именно в связи с бытием предмета познания, значит открыть дорогу к посильному мысленному моделированию. В этом и состоит задача контекстной обработки предметной информации. Обнаруженные формы позволят отказаться от номинально-репродуктивного обучения в пользу обучения эвристического.
Литература
Гайдук Ю.М. Как решать задачу./Математическое просвещение, Вып.1.– М.: ГТТЛ, 1957. С.256
Киселёв А. Элементарная геометрия для средних учебных заведений. С приложением большого количества упражнений и статьи: Главнейшие методы решения геометрических задач на построение.– М.: Т./Д. «Думнов, Клочков, Луковников и К°», 1913.
Литцман В. Теорема Пифагора. – М.: ГИФМЛ, 1960.
Лосев А.Ф., Тахо-Годи А.А. Платон и Аристотель. – М.: Мол. Гвардия, 1993.
НАЧАЛА ЕВКЛИДА. Книги I-VI.– М.-Л.: ГИТТЛ, 1950.
Платон. Сочинения в 4-х томах. Т.4. – М.: Мысль, 199
Плутарх. Сравнительные жизнеописания в 2-х тт., Т.2. М.: Наука, 1994.
Шереметевский В.П. Исторический очерк развития анализа и его приложений к геометрии. В книге: Лоренц Г. Элементы высшей математики. Т.1. – М.: Т-во И.Д. Сытина, 1910.
Шоке Г. Геометрия. – М.: Мир, 1970.